Build Your Own Hyperbolic Soccer Ball Model
Sending off Euclid
Keith Henderson
The traditional soccer ball is made of arrays of hexagons gathered around central pentagons. The hyperbolic soccer ball model is simply an array of hexagons gathered around central heptagons. Follow these directions to construct a hyperbolic soccer ball model of your own. Warning: the finished product will not be ball-shaped. A model built correctly will look something like this:
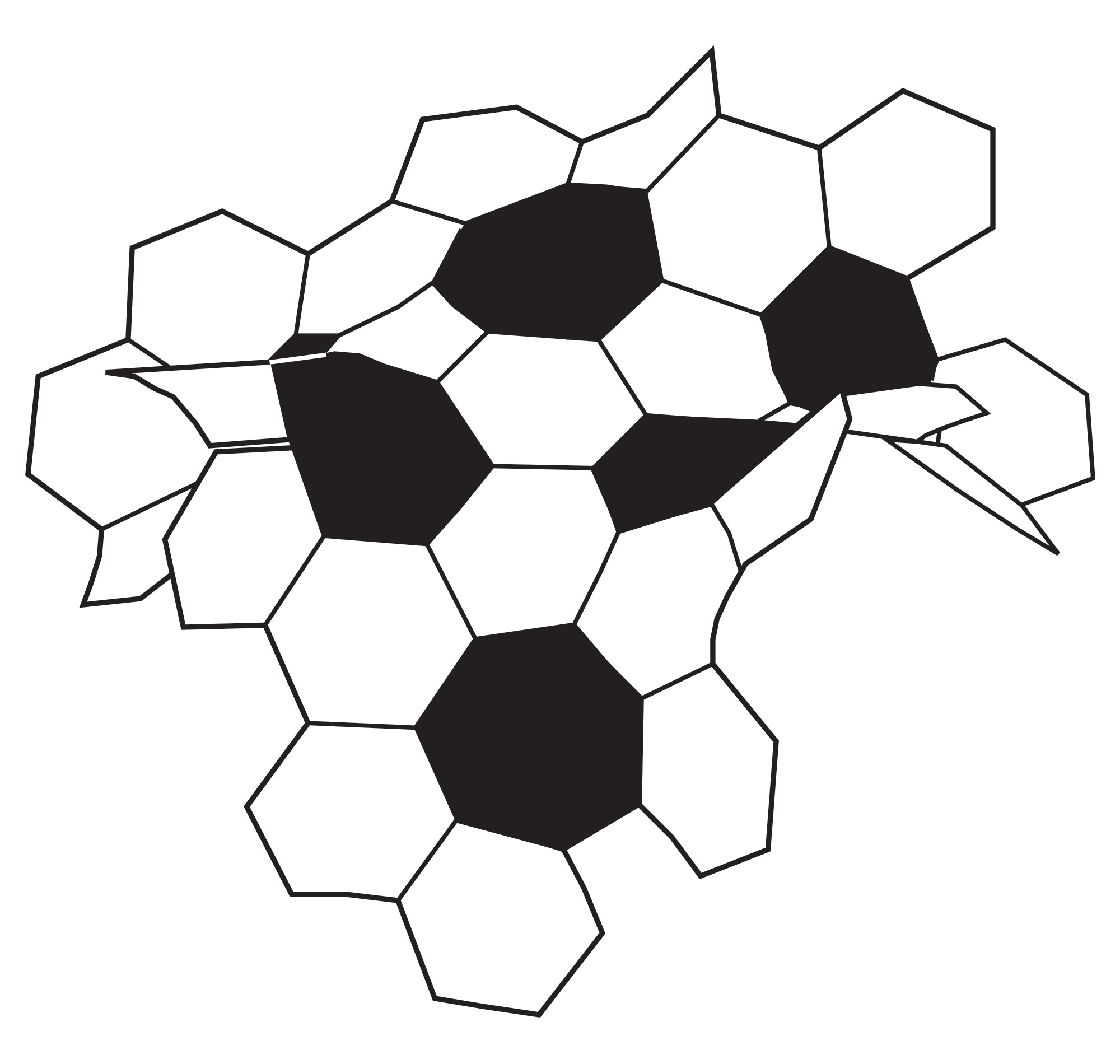
Directions:
Start by printing three copies of this PDF. Use colored paper if you like.
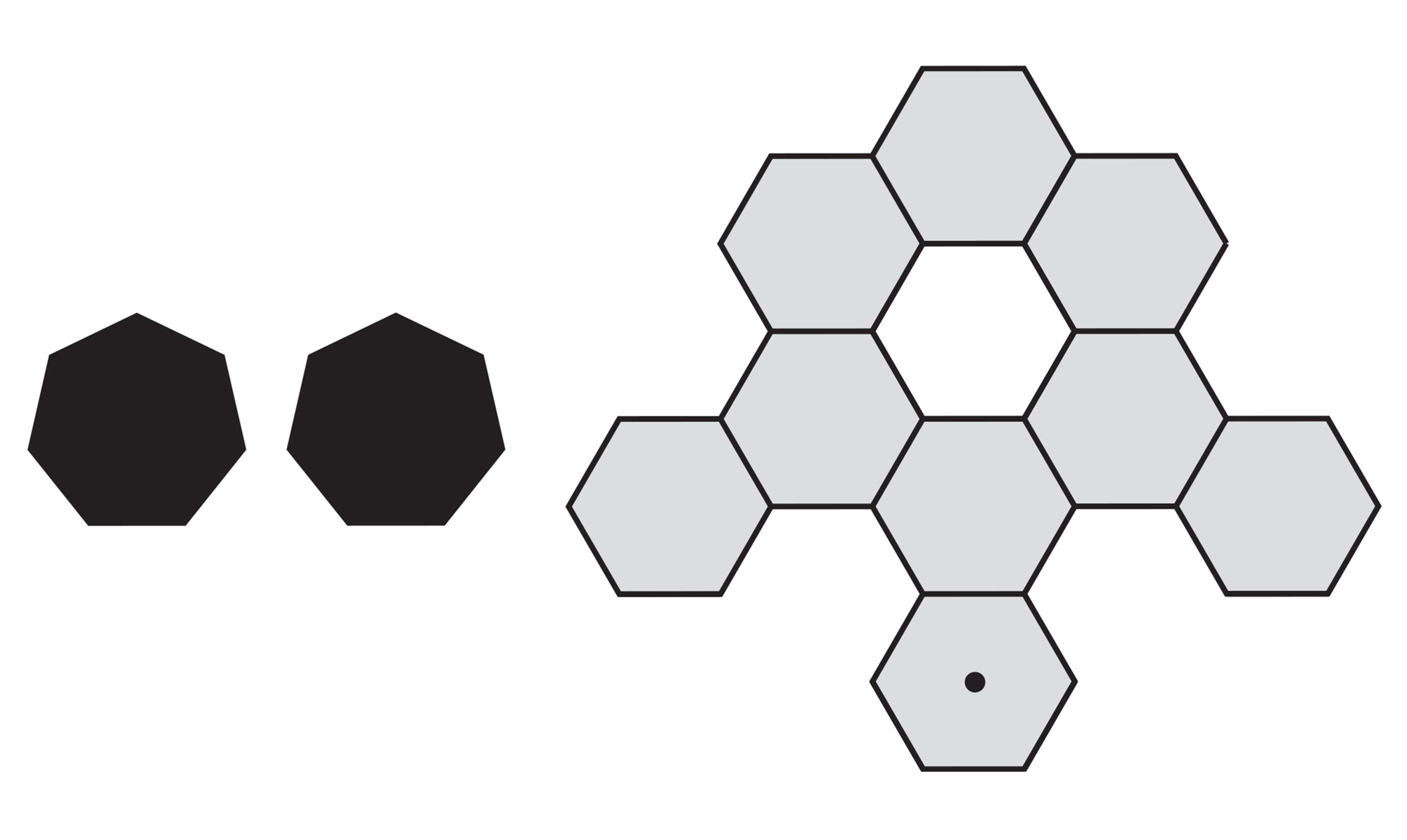
On each of the three sheets, cut out the two black heptagons. Then cut out the larger irregular figure, making sure to cut all the dotted lines and only the dotted lines. Each sheet should yield two black heptagons and one irregular figure with a hexagonal hole in the middle:
Take the three irregular figures and arrange them in a kind of triangle. The hexagons containing dots should be at the center of this triangle arrangement:
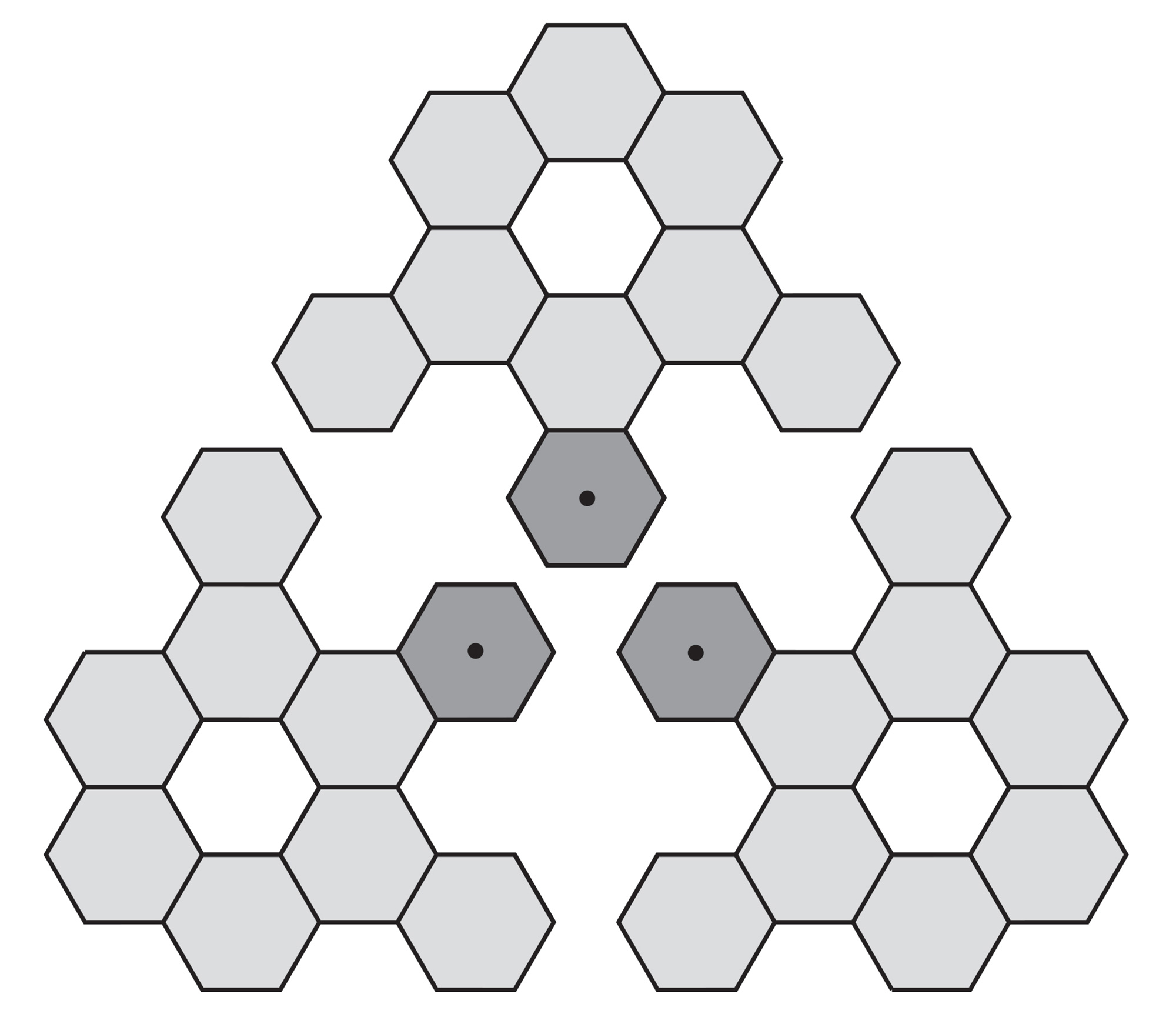
Put the three hexagons containing dots on top of one another, and tape these three hexagons together. You will notice that other hexagons are overlapping, too. Do not tape these other hexagons together! You should now have this:
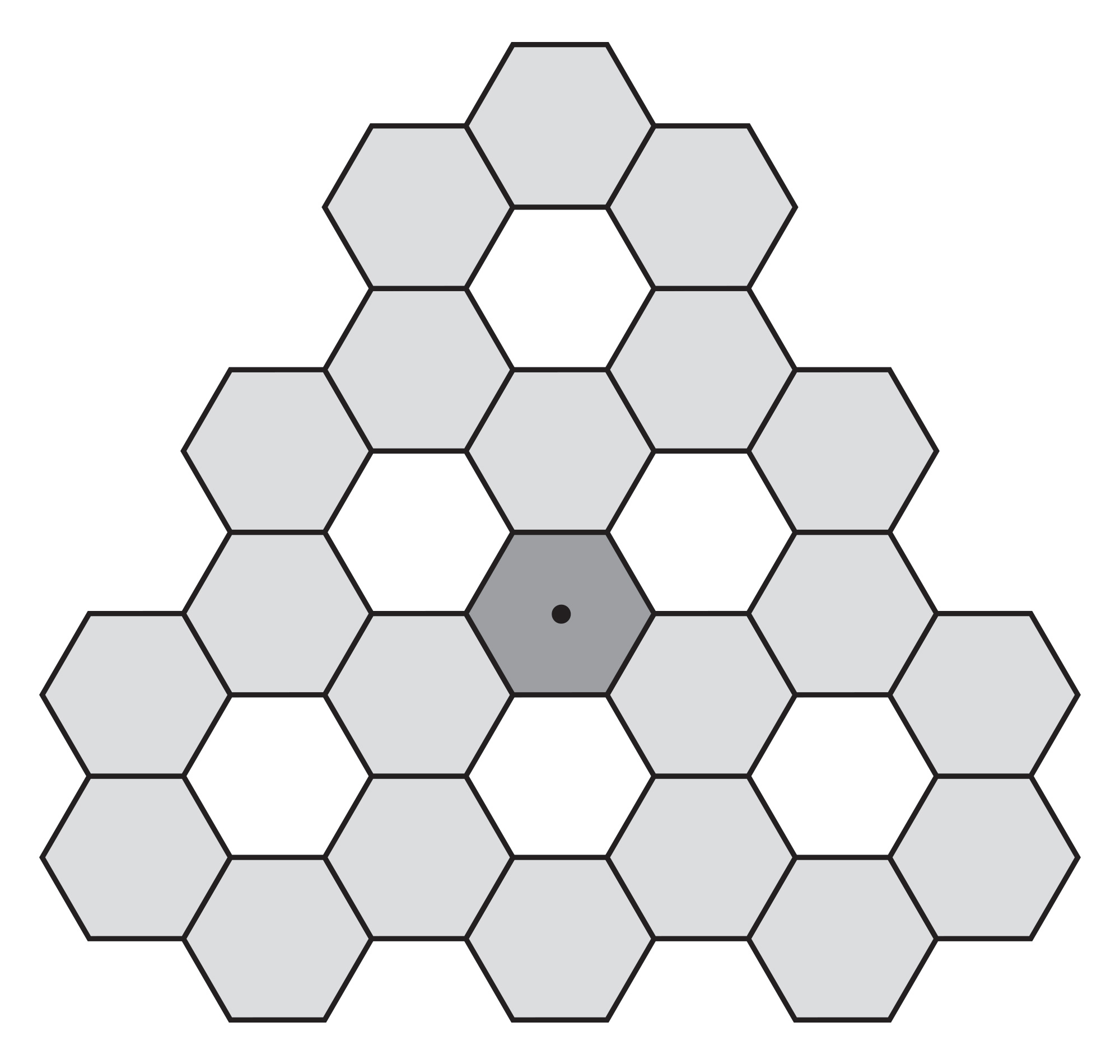
Grab a black heptagon and insert it into one of the hexagonal holes near the edge of your irregular shape. To properly insert the heptagon, you will have to widen the hole, spreading hexagons apart, warping the surface of the paper in an unusual way:
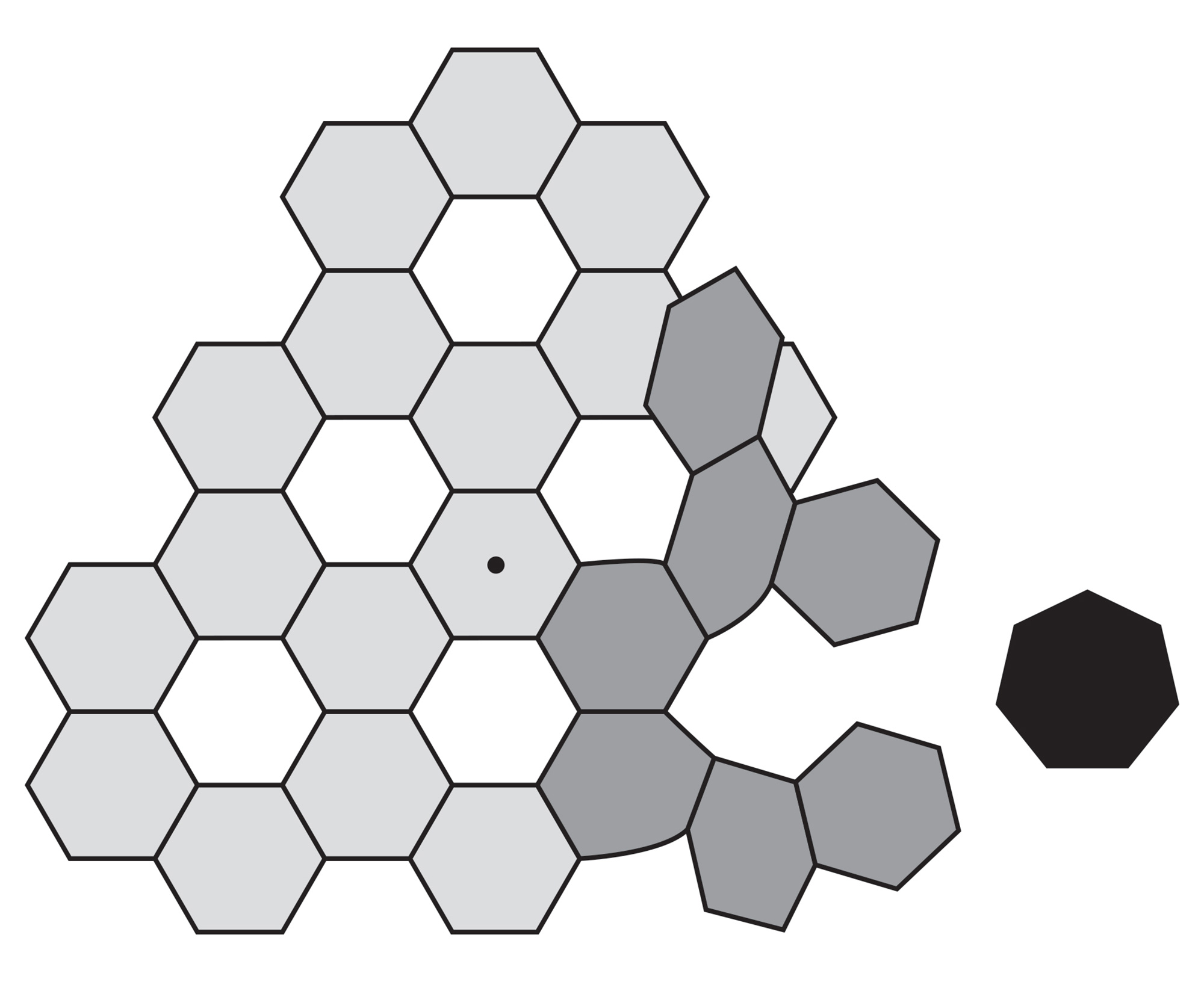
Tape the heptagon into the widened hole, making sure that each side of the “hole” matches one side of the heptagon:
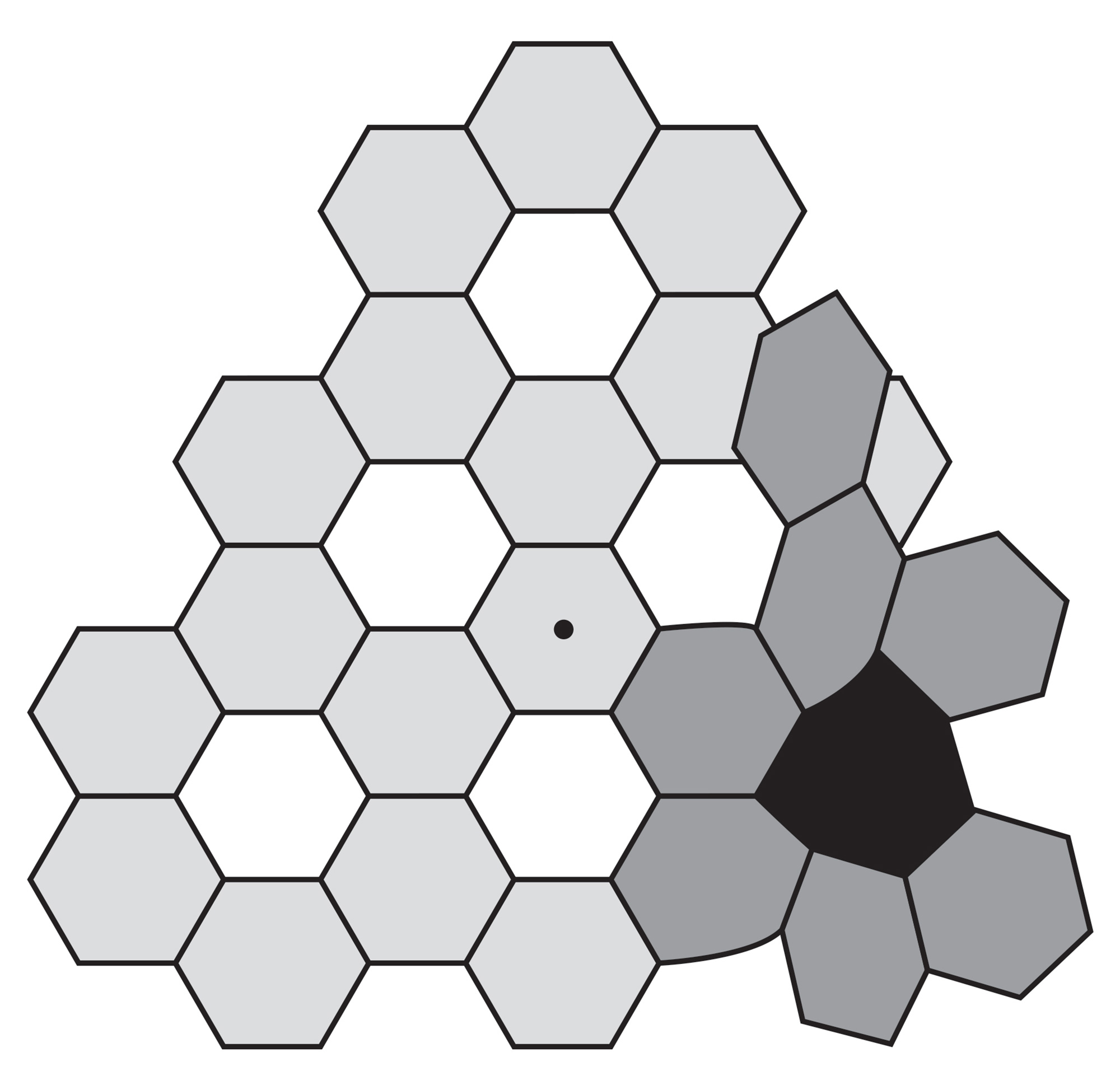
Fit the remaining five heptagons into the remaining five holes using the “hole widening,” “paper warping” technique you just learned. In some cases, you will have to spread apart overlapping hexagons. See the top image for hints.
If you’ve come this far and you want to continue, you may. Just photocopy more shapes and add them to the edges. (A little playing around will reveal correct orientations.) The more shapes you add, the more the hyperbolic structure will become apparent.
Keith Henderson is professor of mathematics at the Department of Mathematics, Cornell University. He is the co-author (with Daina Taimina) of Experiencing Geometry: Euclidean and non-Euclidean with Strands of History.