To Be or Knot to Be

“To be, or not to be.” ­The most famous words in the English canon. But what, exactly, is the question? For Hamlet it appeared as a matter of life or death, but in modernists such as Samuel Beckett, Thomas Bernhard, and Elfriede Jelinek, we encounter situations in which, though the “I” of the text is clearly alive, it finds itself, in some way, radically negated. In such states, it is not clear that there is any substantial difference between being and not being. Faced with this thoroughly modern dilemma, how might we proceed?

As this is a problem of both being and language, perhaps we should begin with the words. “To be, or not to be: that is the question.” We have already seen that in existential soul-searching, the shift to modernity requires, in the second half of the proposed dilemma, the substitution of a w for the t. This shift produces the new formulation, “To be, or not to be: what is the question?”, the problem no longer being whether to simply be here or not, but whether we can still say that there is any real difference between these apparent choices. If the second half of the assertion has undergone a semantic shift, might not the first part also require modification if it is to adequately register the most recent findings in how we define subjectivity? In line with this hypothesis, might we not propose that the thoroughly twenty-first century version of Hamlet’s dilemma is: “To be or a kNot to be: what is the question?” And the question is: What is the question here?


Clearly, our updated formulation of the existential dilemma is rather complex, not to say, positively paradoxical. We should not then be surprised that there is no general consensus on what is at stake in this question, let alone anything like an agreement on an appropriate method for addressing it. However, many notable writers, poets, philosophers, and social theorists have put their critical capacities to work on the problem. Of this plethora, one of the more intriguing is that proposed by the French psychoanalyst Jacques Lacan.

In the beginning was what’s kNot. 

Then God said, “Let the kNot be.” 

And It was. 

And It was a Borromean Knot.


Though Lacan’s approach to the analysis of the psyche was originally inspired by the anthropologist Claude Lévi-Strauss, who had successfully applied group theory to the analysis of kinship systems, and more contentiously to myths, Lacan was no ordinary structuralist, and could not stop at mere group theory. Appropriating geometry, topology, and eventually knot theory for his notion of the psyche, in the early 1970s Lacan settled on a model in which psychic reality is (re)presented as a complex of three separate, but interrelated spheres: the Real, the Symbolic, and the Imaginary. 


In this model, the three rings do not represent boundaries of areas on the plane; the figure is not a set diagram. Rather, the rings represent rims, or holes in a “body,” around which desire flows. Lacan’s idea here is that the psyche is itself a “body” or space whose boundaries are defined by its rims, just as we can say that, from a topological perspective, the space of the physical body is defined by the rims of its orifices—the mouth, nostrils, eye sockets, earholes, anus, and vagina. The difference with psychic-body space is that its rims are not dispersed across a surface, but are twined into a “knot,” which lies at the center of the being. The figure that these rims form, the navel of Lacan’s psyche, is known technically as a Borromean knot.


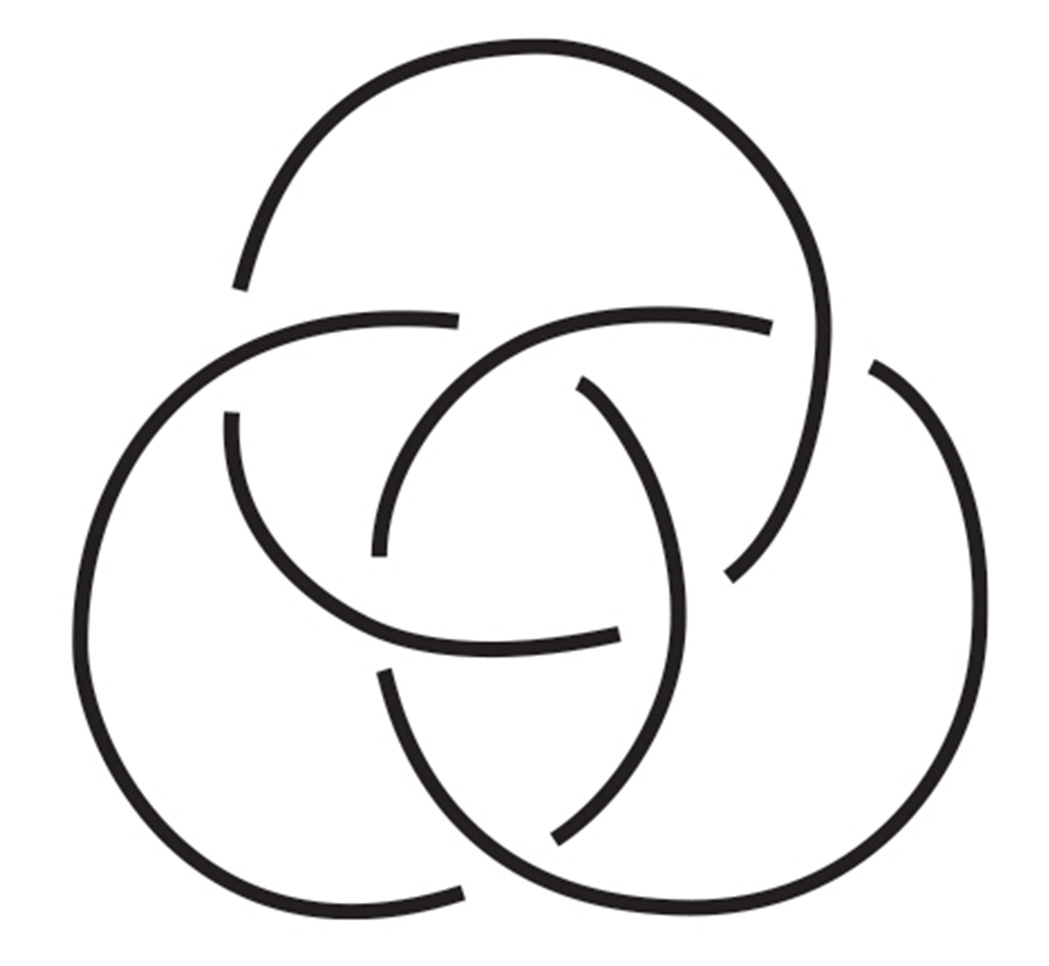
As Colin C. Adams states in the Knot Book, his enormously accessible and erudite introduction to knots, in contemporary mathematical parlance, knots are objects composed of a single “closed curve in space that does not intersect itself anywhere.”^[2] Objects like the Borromean, which are composed of more than one interlinked element, are thus not technically knots but rather “links.” However, the longevity of the Borromean figure’s designation as a knot means that it is interchangeably known as the Borromean knot, the Borromean link, and even the Borromean rings. The shape of the rings does not effect the configuration. They can be round or square, made of DNA chains, laurel branches, or lines in hyperspace. What matters is simply that “to undo one is to undo them all.” We may also add a fourth ring to the configuration, to derive a figure known as the Borromean lock, a figure to which we will return later. Interestingly, though Borromeans seem to occur in both two and three dimensions, in reality, they are all three-dimensional. The two-dimensional version is just an image, a projection or shadow, of the three-dimensional form. 


Whatever its technical designation, the adjective “Borromean” derives from the object’s association with the family of Borromeo who added the three-ringed link to their crest in the fourteenth century. In the early-fifteenth century, when Francesco Sforza, who had inherited the family’s estates, was made Duke of Milan, he gave permission to other noble families to use it on their crests, as a sign of his expanding domain, though technically it designates only the region around Cremona. Consequently, the rings can be found on many monuments in and around Milan: inside and outside, on floors and ceilings, in the shapes of the windows, and engraved on architraves. Sforza Castle, Francesco’s elaborately fortified manse, is covered in them, though photography is not allowed on the premises.


But long before this aristocratic family co-opted the form, its image had appeared in many cultures around the globe and across the ages, in particular in connection with religious beliefs and practices. “A form of the Borromean link was used by the Norse people of Scandinavia. The symbol known as ‘Odin’s triangle’ or the ‘Walknot’ (meaning ‘knot of the slain’) has two variants. One is a set of Borromean triangles; the other is a unicursal curve that forms a trefoil knot. … [It] is associated with the Norse god Odin. Scenes on picture stones show fallen warriors traveling to the next world by boat or on horseback where they will join others in Odin’s palace, Valhalla—the castle of the slain. Hovering in space above the dead, the Borromean/Walknot signifies the passage to this ‘other’ place.”^[3]

For many centuries now, the Borromean rings have also been used to depict the mystery of the Christian Trinity. “The earliest source for this that we are aware of was a thirteenth-century manuscript in the Municipal Library at Chartres. It contained four diagrams. … In the centre, inside all the circles, is the word ‘unitas’; the three syllables of ‘tri-ni-tas’ are distributed in the outer sectors.”^[4] Borromeans have also been found in non-western cultures such as that of the Shinto religion in Japan, whose mythology divides the world into three realms: heaven (the land of gods), earth (the land of man), and the underworld (land of the dead). Their interconnectedness is represented by the three interlinked circles, which can be found all over ancient Shinto shrines such as O-Miwa Jinja. Lately, Borromean-like figures have also been found in natural phenomena, e.g., the molecular structure of certain chemical substances. But though the figure, and many other different kinds of knots and links, have appeared in a wide variety of cultures and conditions, it was not until the late-nineteenth century that mathematicians began to study them seriously.^[5] Now more than a century old, knot theory is one of the most dynamic areas of modern mathematics. The study of knots has led to important applications in the synthesis of new molecules and in DNA research, and is now widely used in statistical mechanics and quantum field theory. It can also help us further our understanding of the psychic cosmos.

We have already seen how in Lacan’s original knotty model, the psyche is (re)presented as a space bounded by the three interlocked rings of the Real, Symbolic, and Imaginary. However, in 1975, after his long encounter with the writings of James Joyce, Lacan felt compelled to add a fourth ring to the configuration, turning it from a link into a lock. Called the sinthome (one of Lacan’s many plays on words), this fourth element—the symptom—is what keeps a psyche locked up. From this perspective, the aim of Lacanian analysis is to unlock the link by breaking the sinthome’s hold—that is, to untie the fourth ring and let the psyche be, as simply as it can, a three-ring knot. “To be knotted otherwise, this is what is essential to the Oedipus Complex and it is precisely [this on which] analysis operates.”^[7]

Analysis then, as a practice, rather than a theory, is for Lacan simply the operation of this unlocking—the separation of the sinthome from the body of the psychic link. The analytic situation may thus be represented by a diagram in which two Borromean knots—a lock and a link—are conjoined.


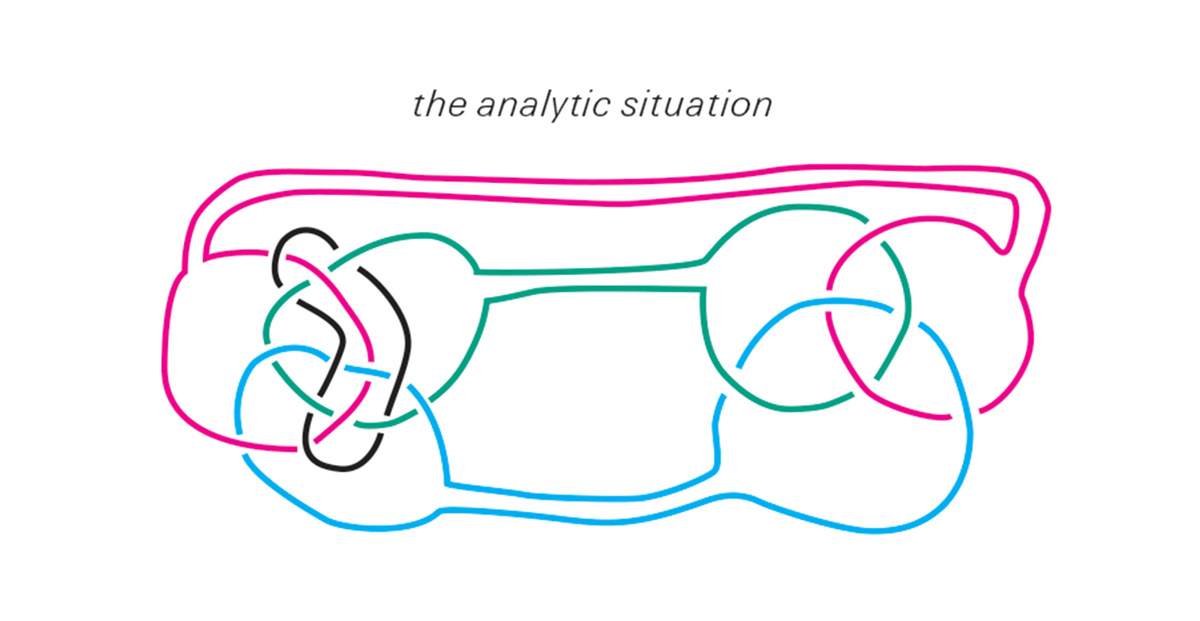
The knot, on the right, represents the analyst who, having herself already shed her sinthome, has only three rings in play. The other, on the left, is the analysand, whose sinthome is still locked into the subject. In an article entitled “The Topological Dénouement of the Cure,” the analyst/mathematician Robert Groome states that this configuration can be topologically transformed—morphed without cutting—into two Borromean links, with the fourth ring of the analysand’s sinthome dropping out in the process.^[8]

In other words, according to Groome, the analytic cure is a topological operation in which two knots join so that one can become unlocked. As Groome nicely phrases it, this unlocking process of separation is not a negative experience, but a “positive moment of dénouement.” However, this denouement does not render the analysand tangle-free, insofar as what is left is still a knot, or at least a link. Furthermore, the ring of the sinthome does not disappear; it simply detaches itself from the other psychic rims. In this way, we may say that the analytic operation does not free one from entanglements; rather, it frees one into a new kind of knot, one that is structured as a link, not a lock. But if the psyche as a whole is composed of a space plus its boundaries, and if these boundaries can be reconfigured by topological operations, does this mean that the boundaries and the space they define represent two different psychic phenomena? And how does this relate to the tripartite division between Real, Symbolic, and Imaginary?


From the perspective of mathematical theory, knots—which for the purposes of this argument will be taken to include links and locks—are not essentially conceived as holes in space. Rather a knot is a logically autonomous entity that can be studied quite independently of any space in which it may be embedded. However, knots may also be used to construct different spaces. When we do this, the knot is not considered as a hole cut in the space, but rather, as alluded to above, is seen as the boundary by which the space is defined. A space defined by a knot, including links and locks, is known technically as a knot-complement. A knot complement is what’s left when a knot is either entirely removed from a space, or pushed away to infinity. The latter case does not lead to a situation in which, if we just kept going, somewhere out there, we’d finally run into a giant knot. The space is called a knot-complement because the knot has effectively been removed from it (the result of shoving it off to infinity). No matter how long you traveled, or how fast, you would never reach the rings of the knot itself. As you headed for where these would be, distances that look small to an external observer would actually become extremely large and you would never reach the edge.^[9] There is now intense mathematical interest in knot-complements, because they have amazing properties. Borromean knots also have complements, but before investigating the specific qualities of such a space, we should first make a more clear distinction between the knot and its complement in Lacan’s topological model of the psyche. In other words, we must now make a clear distinction between the psyche in general, and that specific psychic phenomenon that Lacan called the “Subject.”


In much of his writing, Lacan refers to the Subject as a rim, or edge-condition, around which desire flows. If we combine this notion with the hypothesis of his topological model of analysis, we see that, for Lacan, the Subject is the “rim” or “edge” of the psychic-body space. The “Subject” is the limit-condition where the body of psychic space encounters its own discrete boundaries. In other words, the “Subject” is nothing but the “event” of the psyche becoming aware of its own limits, this event taking place around a rim knotted into the form of a Borromean. If the Subject is thus the knot itself, the knot-complement is an analyzed psyche minus the Subject, that is to say, a psyche that has both shed its sinthome and withdrawn from its fixation on its self. What would be the experience of subsisting in such a space?

The following sequence describes the steps used in the film to arrive at this knowledge.^[10]

1. Imagine the Euclidean space we have all been taught to regard as the model of our physical universe—homogeneous, three-dimensional, stretching infinitely in all directions. 


2. Mold this space into a ball. It’s still infinitely wide in 
every direction; it just has a spherical shape. (Technically, 
to actually do this, we would first have to add a point. As this is just a teensy-weensy dimensionless point, we’ll just consider it done and carry on.)


3. Deform the ball to make a cube.


4. Draw a line, or axis, down the middle of each side of the cube:


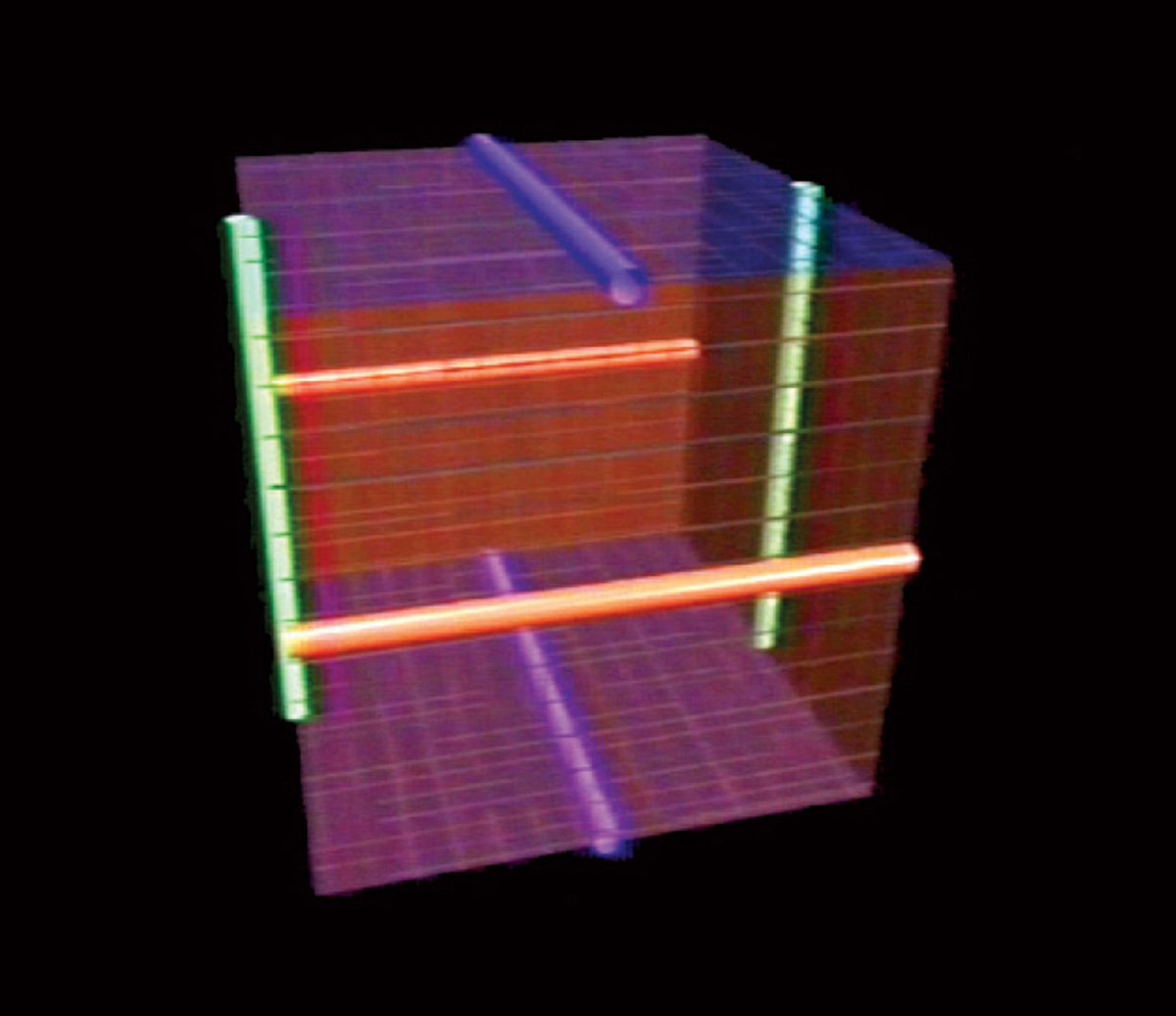
5. Bend each pair of sides so that their two axes join into a loop. The result is a space bounded by three rings linked into a Borromean knot. Note that this knot lies not on the inside of the space but at its outermost edges:


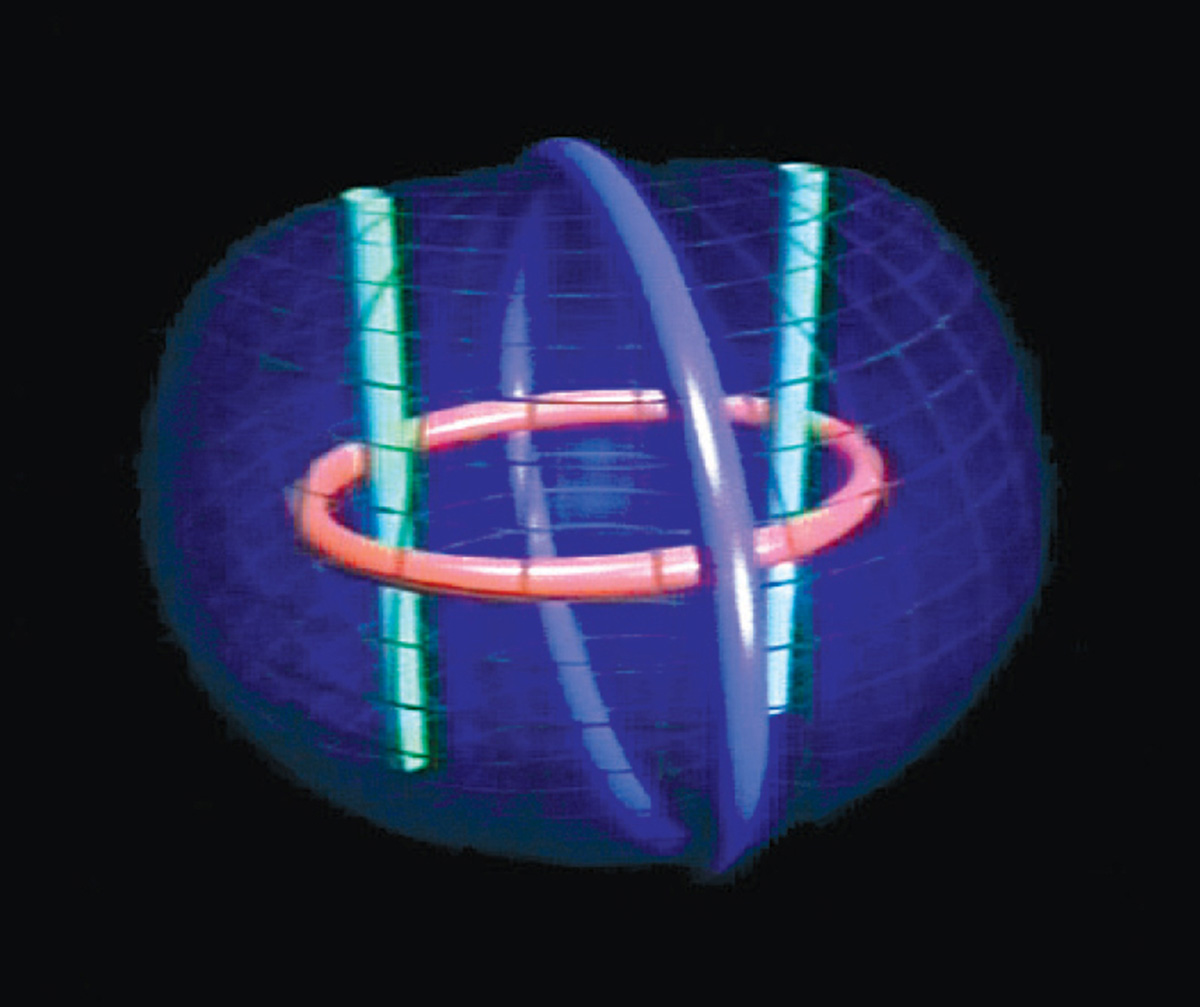
Now comes the tricky part!


6. Imagine that each of these three boundary lines functions as what mathematicians call an “axis of symmetry.” In other words, as well as having the shape of a ring, each axis now acts like a mirror, bouncing back light rays that hit it. Note that these “mirrors” do not lie within the space; they are located as its boundaries. Thus, a light-ray reaching the ends of this space bounces back, giving the illusion that space has been doubled. Remember, too, that we have three of these mirror-boundaries and that each has the shape of a self-enclosed ring.


7. Turning on one symmetry axis of our deformed cube 
produces the appearance of an infinite row of boxes.


8. Turning on two axes of symmetry produces an infinite plane of cubes:


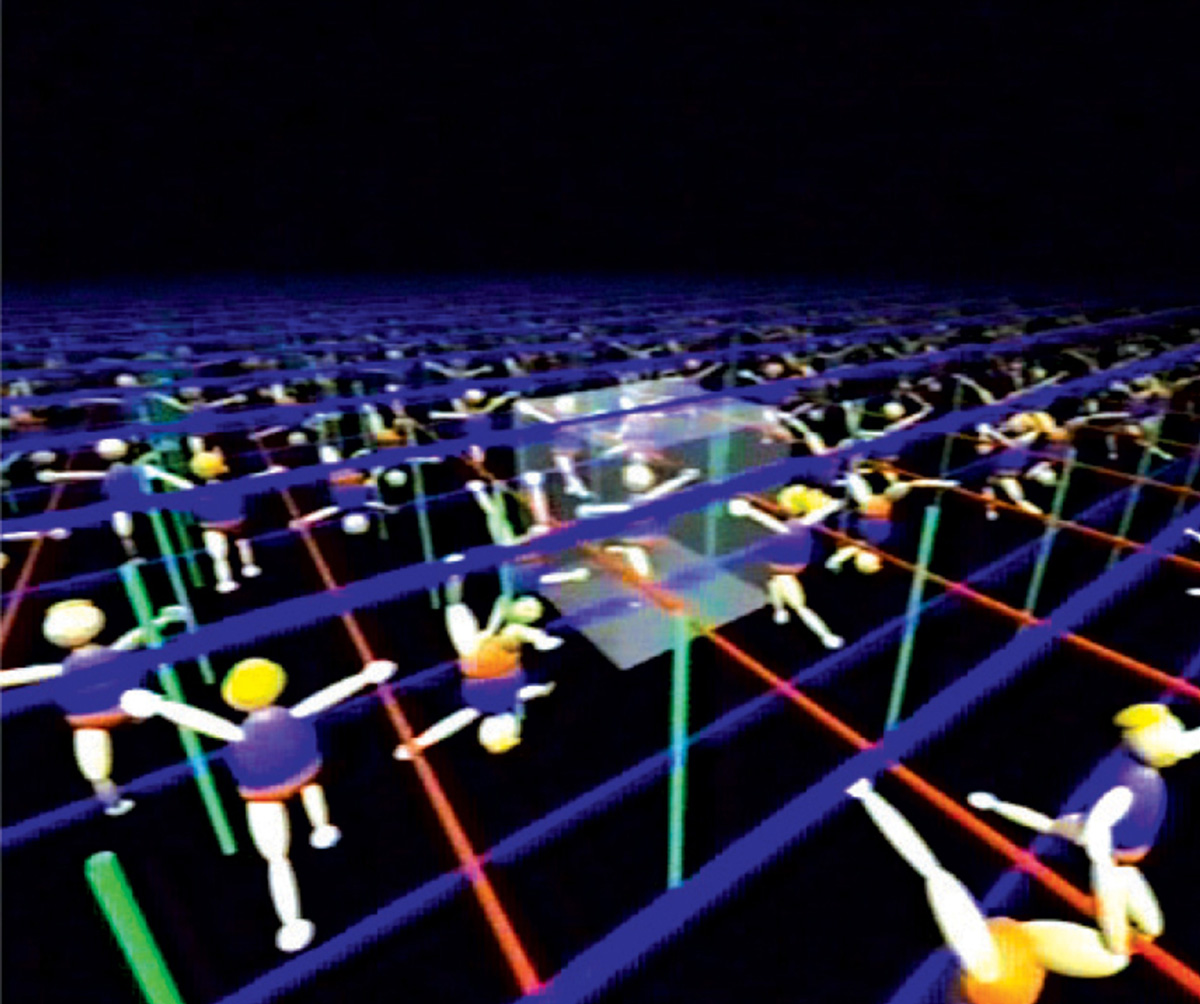
9. Switching on all three axes gives the illusion of an 
infinite volume tiled by cubes, very much like sitting in a Yayoi Kusama Infinity Box:


10. Now repeat steps 3–9, only begin by molding the sphere into a dodecahedron...


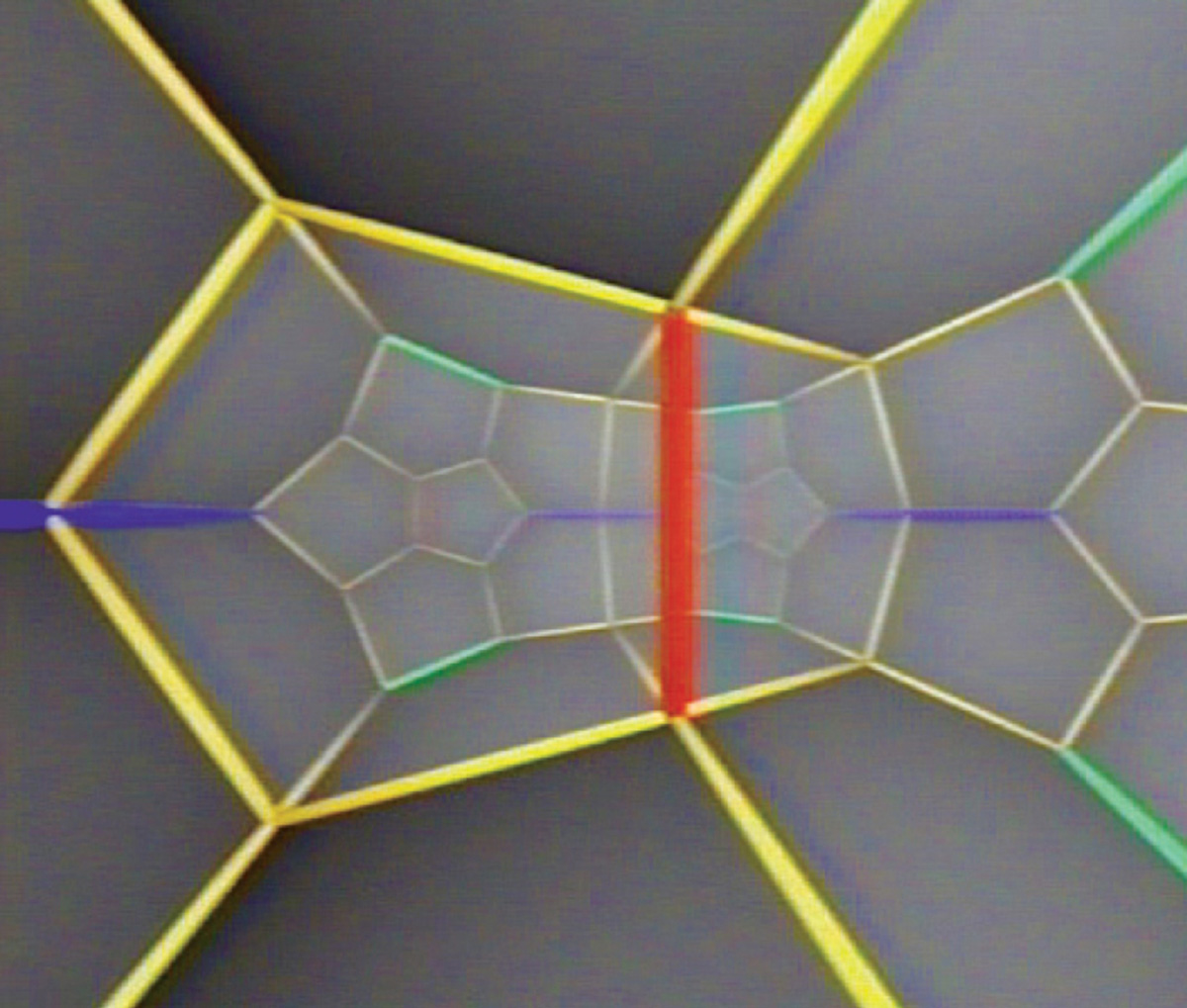
11. ...while also giving each axis the power of four-
fold symmetry, rather than the simple doubling capacity 
of normal mirrors. Note that mathematical “mirrors” 
are not limited to one reproduction of space (as in our material world), but may reflect many times, depending 
on the “symmetry” properties of the mirror. A picture of the resultant space would have a pseudo-crystalline structure in which each cell is a duplicate of the original dodecahedral form:


Such a space would be of finite volume and possibly quite small in relation to the spatial scales commonly associated with cosmological models, and it would contain a limited number of galaxies. But the multi-connected nature of this space would present a virtually unlimited number of images of these galaxies, often referred to as “ghosts.” To an even greater extent than gravitational mirages, these topological mirages would create a vast optical illusion, making space appear much bigger than it really is.^[11]

This is what happens when we have four-fold symmetry. Is it possible that our axes can be given even more reflecting power? Say 10, 11, 20, 1000-fold symmetry? What about infinite reflectivity? As it happens, the answer to this question is yes, if we allow that the space occupied by our dodecahedron can be hyperbolic, rather than Euclidean.^[12] In this case, if we keep decreasing the angles at its vertices indefinitely, the axes of reflection are pushed further and further away, causing the symmetry to increase. 


When the axes are pushed to infinity, the symmetries also become infinite. The final sequences of Not Knot give us a virtual tour through just such a universe. As we revolve through the space, the points at infinity seem to come closer and closer. Then, just as we expect them to hit us in the eye, they suddenly swerve round the back of our head, and a new vista, with vast bundles of rays receding into the infinite, opens again before us. This is what it’s like to be inside the complement of a Borromean knot.

Although, at the small local level, lived experience offers little support for the idea that the real world conforms to this strange geometry, some scientists have dreamed that at the overall macro level, it might. Sadly, a probe now sending information back from the outer reaches of the cosmos suggests that this is probably not the case. But, if the psyche, sans Subject, i.e., minus an awareness of its own limits, is the complement of the Borromean knot, then psychic space is precisely that described in Not Knot. Thus, if we wish to take a hyperbolic trip, all we have to do, apart from slipping out of our sinthomes, is to withdraw from our fixation on our selves, and relax into the sublime fantasy of a limitless void. Maybe the mystics got it right after all.