A Difficult Pancake: An Interview with Hinke Osinga and Bernd Krauskopf
Making sense of the Lorenz Manifold
Margaret Wertheim, Bernd Krauskopf, and Hinke Osinga
In 1963, Edward Lorenz, a meteorologist and former weather forecaster for the US Army Air Corps, published a paper in the Journal of the Atmospheric Sciences that almost nobody read. Entitled “Deterministic Nonperiodic Flow,” the article was the culmination of his thinking about the phenomena involved in weather forecasting. Lorenz had become disenchanted with the standard mathematical models underlying weather prediction, which assumed that atmospheric phenomena behaved in a linear fashion. In his paper he offered up a non-linear model, outlining what later came to be known as the “butterfly effect.” This article, which was rediscovered by mathematicians in the 1980s, is now regarded as one of the founding works of chaos theory. Lorenz’s radical reassessment of atmospheric dynamics led him to discover an extraordinary mathematical object called a “strange attractor.” It is now known that such attractors lie at the heart of chaotic dynamical systems. The Lorenz attractor itself has become an unofficial mascot of chaos theory. As it turns out, this enigmatic, infinitely complex object is itself associated with a much larger and even more complicated surface known as the Lorenz manifold, a truly bamboozling mathematical object. Mathematicians Hinke Osinga and Bernd Krauskopf—a wife-and-husband team at the Department of Engineering Mathematics of the University of Bristol—have spent the past decade studying the Lorenz manifold and mapping its anatomy. Margaret Wertheim recently interviewed them at Cornell University, where the pair were visiting researchers at the Center for Applied Mathematics.
Cabinet: Could you begin by telling us why anyone became interested in chaos theory in the first place?
Hinka Osinga: Historically, mathematicians believed that if you write down an equation, then you should be able to find a solution given by a nice formula. That’s what Newton and Leibniz, the inventors of calculus, thought in the seventeenth century. Calculus describes systems by their rates of change—one obtains what is called a differential equation, and each of its solutions, specified by an initial condition, is defined as a function of time. As an example, think of a leaf going downstream in a river: you drop it somewhere and it starts moving. The solution is a path that tells you the exact position in the river as time develops. Now, what people discovered in the nineteenth century is that it is very easy to write down a differential equation that has well-defined solutions but, astonishingly, you are not able to express them with a straightforward formula. It’s just not possible. The start of chaos theory is almost at the end of this difficulty, in that you cannot find solutions in this sense for even really simple differential equations. Also, you can show that while solutions must exist, they may have the property that the associated path is unpredictable. That was very surprising.
How does this lead to chaos theory?
HO: The classical example is the motion of planets, which goes back to Kepler and Newton. According to Kepler, a single planet moves around the sun along an ellipse. Now, what happens if you have two planets or three? The motion of any number of bodies relative to one another can be described by Newton’s laws, but it quickly gets very complicated. What exactly is this motion? This was an open problem for a long time. In the 1880s, King Oscar II of Sweden organized a competition for mathematicians, asking for a definitive answer to the question: “Is the motion of the planets stable?” The French mathematician Henri Poincaré showed that as few as three celestial bodies lead to instability.
This is the famous “three-body problem.”
HO: Yes, indeed. Poincaré discovered that this system is impossible to predict. It’s about whether the motion of the planets is truly periodic. The earth goes around the sun and every year it does the same thing. We like that. But if you look at the planetary system as a whole, is its motion truly periodic? It turns out that it’s not. If you look at the very long timescale, there is an unpredictability and you cannot tell precisely where all the planets will be relative to each other. That is the birth of chaos theory.
So this word chaos, which sounds to most people as if it means that there’s absolutely no structure, is in some sense a misnomer.
Bernd Krauskopf: Everybody has a notion of what chaos means—something completely unordered—it’s even there at the start of the Bible. But from a scientific point of view, when we talk about chaos theory what we mean is the notion of deterministic chaos. It’s a bit technical. The classical idea that mathematicians had is that if you knew the behavior of the system for one initial condition then the behavior for nearby initial conditions would be very similar. But in chaotic systems, that is not so. What we have come to understand is that in such systems even the tiniest changes in the initial condition—beyond anything we could ever dream of measuring—can have an enormous influence on the dynamics of the system after a very short period of time. One speaks of the “predictability horizon” here. If a system is chaotic, there is a certain horizon up to which you can say with some certainty what the system will do, but then after this horizon, that’s no longer the case. So even if you measure your initial conditions with all the precision we have in the world, you will still not be able to predict what the experiment will do in a few seconds or a few days or a few weeks.
This is the “problem of sensitive dependence on initial conditions,” also known as the butterfly effect. Can you describe that a bit more?
BK: It’s attributed to the meteorologist Edward Lorenz. The idea is that the weather is so sensitive that if a butterfly flaps its wings in Brazil, there could be a tornado in Texas as a result. Of course, it’s not the fault of the butterfly. It just means that an influence as small as the flap of a wing can have, after a few days or weeks, an effect that we cannot predict. Lorenz was trying to understand how weather patterns develop. He wanted to know what the weather is going to be tomorrow, or next week. The equations he developed—which are arguably the most famous equations of chaos theory—were a way to explain a very basic concept that we can all observe. When you have something heating up—such as when you boil water in a pot—what you see is the water going around in circles, coming up and going back down. You have a scroll in one region going one way, and another scroll going in exactly the opposite direction. These are called convection cells and the atmosphere does something similar. Lorenz’s equations use a very simplified model of convection, and he effectively showed with these equations that the intrinsic impossibility of predicting the weather stems from very simple concepts.
From these equations, he discovered his famous Lorenz attractor. What is an attractor?
HO: One way to look at the Lorenz system is to forget that it comes from some approximation of the atmosphere, and to see the equations simply as differential equations. You can think of them as describing the motion of a particle in “state space” under the influence of a force field that is given by these equations. [A state space is a multidimensional space in which each variable being mapped is represented by its own dimension. —Eds.] Lorenz discovered that whatever initial condition the particle starts from, it will eventually end up within a specific region, or “box,” of the state space. Hence, it is attracted to something inside that region, something that mathematicians call an attractor.
So we’re talking about some kind of meta-behavior?
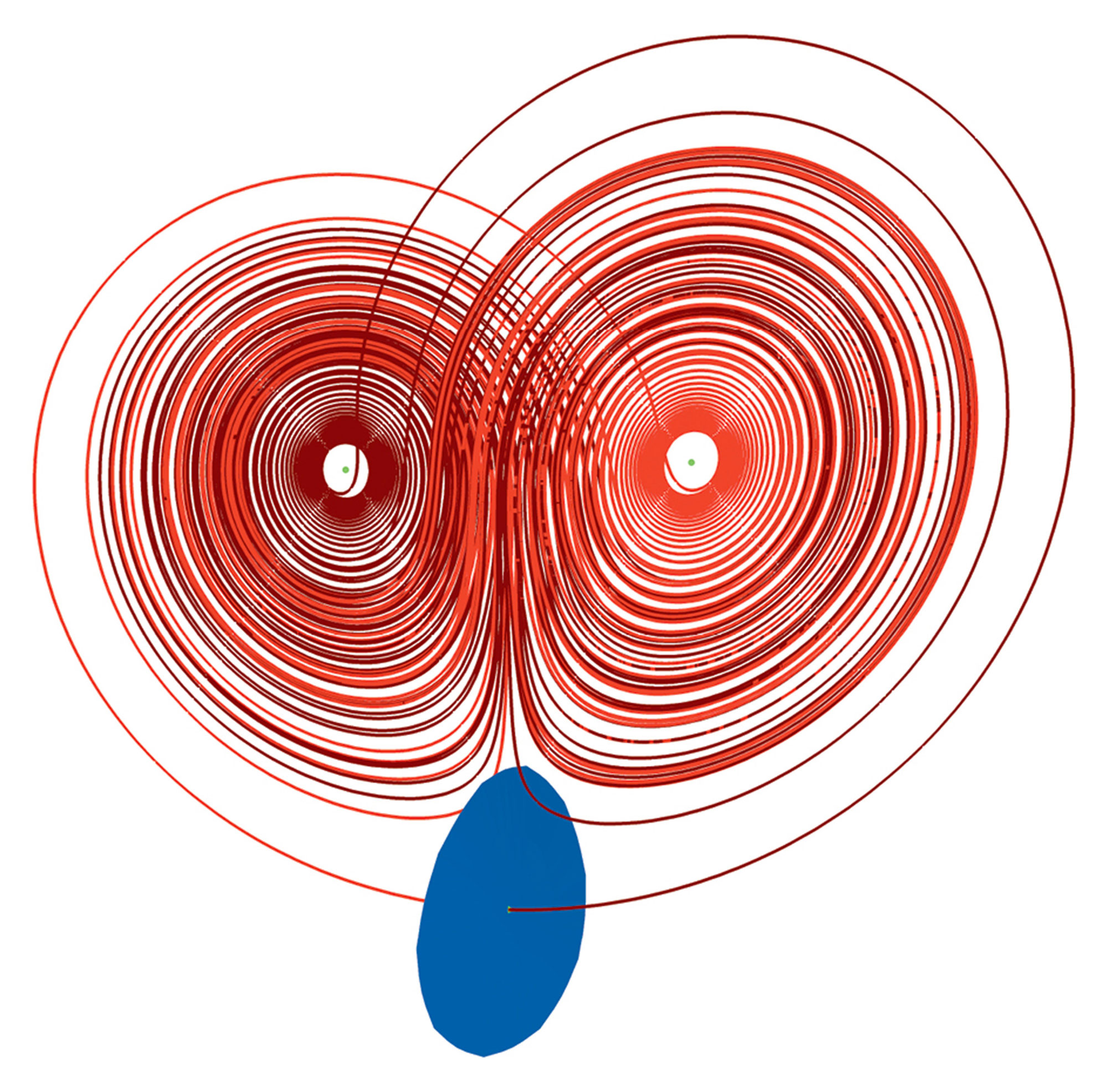
BK: You could say that. Now the question becomes: what kind of object is the actual attractor within the box? What Lorenz discovered is that it is a very strange object, unlike anything mathematicians had encountered before. A solution path on the attractor spirals around and away from one point until it switches over to spiraling around a second point. This switching occurs at irregular and unpredictable moments in time. What is more, any two solution paths on the attractor do this differently. The overall structure looks a bit like a butterfly with two wings. And forty years later, we’re still trying to understand this object and how it organizes things inside and outside the box. That is what our work is about. We are trying to understand the total dynamical behavior that is organized around this strange shape.

How did Lorenz begin to work out what the shape was?
HO: It’s tricky to explain. What he tried to do is use a computer to do numerical experiments of what was happening inside the box. The box is three-dimensional, but he looked at what happened in just a horizontal cross section, a two-dimensional slice of the box. He looked at how a particle passes through the cross section and plotted the places where it crossed through the plane. And slowly he began to see a structure emerging—his chaotic attractor.
BK: So we have to come back to the question of what we mean by solving an equation. You normally think of an equation as having an explicit solution that we can write down with a formula. In that sense, Lorenz’s equations cannot be solved. But for any given initial condition, there is a solution path: if you let the system go and simply watch what happens, this path is a nice, smooth, roller coaster-like curve that you can plot on a computer.
So this becomes a different way of doing mathematics—it’s visual and pictographic rather than symbolic.
BK: Lorenz had a really good understanding of what the attractor looked like, but computer graphic output at the time was very limited, so basically he just had lists of numbers. Today, you can do this on a PC or you can look it up on the Internet—you’ll get all kinds of pictures of the Lorenz attractor online.
HO: The pictures people show are somewhat misleading. The Lorenz attractor is not a single curve. It contains millions of curves and when you put them together you get an infinite number of sheets! Since Lorenz’s first efforts, people have been thinking about different ways to describe what this object really is.
What sorts of real-world problems does this object relate to?
BK: The Lorenz system itself is an idealization; it’s not directly applicable to other situations. But many physical systems show the same flavor of chaotic dynamics. Examples are periodically driven systems, such as when you take a pendulum and drive the pivot periodically. The Lorenz system is a paradigm for the kind of dynamics you can expect. There is one concrete system that does behave exactly like the Lorenz system: a chaotic water wheel. This wheel is tilted and water flows at a constant rate onto its highest point. The wheel’s cups leak water, and the wheel switches at irregular intervals from rotating right to rotating left—just like a solution path on the Lorenz attractor. Actually, mathematician Steven Strogatz here at Cornell has built one.
Is there a whole class of these strange attractors?
BK: You find them all over the place. They all share certain properties and they all look a bit different. In the Lorenz system, there is spiraling around two points, so his strange attractor is sometimes called the butterfly attractor. There’s another famous one called the Rössler attractor that does not have this property: its solution paths spiral around a single point. There are all kinds of others.
You’re mathematicians, not physicists. Why are mathematicians interested in all this?
HO: The origin of this problem comes from a time when the difference between physics and mathematics didn’t exist. If you think chaos theory is physics, that’s fine with me, but you shouldn’t really put it in a box like that.
BK: One could say that the Lorenz system has been fascinating for mathematicians because it allows us to nail down what it really means for a system to be chaotic in a well-defined sense.

You both study an object related to the Lorenz attractor called the Lorenz manifold. What is this?
HO: We baptized it the Lorenz manifold. The mathematical terminology is that it is “the stable manifold of the origin of the Lorenz system.” For short, the Lorenz manifold. Unlike the Lorenz attractor, which is one-dimensional, this manifold is a two-dimensional sheet that’s all twisted and rolled up in very complex ways. It is a surface that has two sides. If you pick a point on one side of the Lorenz manifold, say, on the left, then the solution path first goes to the left wing of the butterfly attractor. If you start on the other side, then the path first goes to the right wing of the attractor. In other words, the Lorenz manifold acts as a dividing sheet between these two types of motion. If you know where you start relative to this surface, you converge to the Lorenz attractor in a particular manner.
So the Lorenz manifold is giving you information about what is happening anywhere in state space, and not only on the Lorenz attractor itself. What’s fascinating about this—because we are not supposed to be able to predict when we go left or right in the Lorenz system—is that there must be something very complicated about this surface that makes it impossible to say whether we’re on the left or the right side of it. It turns out that’s because the Lorenz manifold rolls up in a very intricate way. You can imagine this a bit as if you were folding and rolling up a sheet of fabric over and over again, and then picking a point somewhere inside. Now you have to decide: is this point on the left or the right side of the sheet? It’s very hard to tell. Our work is about trying to understand the properties and the geometry of this surface.
BK: Here’s another way to think of it: imagine a smooth surface that’s like an infinitely growing pancake—a pancake that’s extremely complicated in its foldings. It’s so complicated that if you pick any two points you can think of in space—no matter how close together they are—this pancake will come between them. That’s an amazing property! It also explains why it’s so difficult to calculate.
You are like botanists who’ve discovered this exotic new species and you’re trying to understand its anatomy.
BK: We are asking what this surface looks like. If you try to picture it in your mind, it would be very difficult. But here we have an equation, and we can calculate the surface associated with the manifold. It’s equivalent to understanding the total dynamics of the Lorenz system. We have developed computer methods to calculate the surface in approximation, which is not an easy task.
HO: We use the computer to try to visualize this object and we also use a lot of mathematical theory. It’s a bit of a to-and-fro process: if this happens, then the manifold must have these kinds of properties. Once it has these kinds of properties, then you must also be able to find something else in it, so then we go and look for that in our visualizations. We’re piecing together these arguments from the theory and by using numerical computations.

An analogy comes to my mind that before anyone pointed a telescope at the stars, people just had to look at the heavens with their eyes and try to work out what was going on. Then the telescope became a powerful tool for seeing these objects more closely. In your work, the computer seems to be a tool for seeing this mathematical object more closely. Now, we can actually visualize it. Would you say a picture is worth a thousand words?
HO: Absolutely. There’s always been a bit of a duality—algebra is the art of solving equations just by writing them down on paper, using x’s and y’s and so on. Geometry is more like: What would the intersection of a sphere and a cube look like? And then you just draw it, or construct it on paper. You go the visual way of showing all sorts of properties. Of course, you could also write down the equations of these objects and start developing properties from that by using the algebra. But I’m definitely one of those people who think the picture tells it all. Not everybody’s like that.
Looking at your pictures of the Lorenz manifold, I cannot help but be struck by its almost mystical properties. It’s almost impossible to believe something this beautiful and complicated can be described formally. You spend a lot of time dealing with its technicalities; do you ever look at it and just feel awe?
HO: Absolutely. From an aesthetic point of view, it’s beautiful. For us, it’s awe-inspiring too; maybe at a slightly more mathematical level. For us, we have this pancake that we compute, and it grows bigger and bigger and fills the space. Once you look at it, it’s like: How can it possibly do that? The beauty that other people see in it is in some sense the beauty we see. It speaks to you. It has this shape. Why does it have this shape? What is it? We see the beauty but also what it means. It’s not just some surface that somebody made up; it is intrinsically connected with the question of what chaos is.
Bernd Krauskopf is a professor of applied non-linear mathematics at the Department of Engineering Mathematics, University of Bristol.
Hinke Osinga is a reader in mathematics at the Department of Engineering Mathematics, University of Bristol.
Margaret Wertheim is a a Los Angeles–based science writer. Her books include The Pearly Gates of Cyberspace (Norton, 1999) and the forthcoming Physics on the Fringe (Walker & Company, 2010). She is the founder of the Institute For Figuring, an organization devoted to the poetic and aesthetic dimensions of science and mathematics.
Spotted an error? Email us at corrections at cabinetmagazine dot org.
If you’ve enjoyed the free articles that we offer on our site, please consider subscribing to our nonprofit magazine. You get twelve online issues and unlimited access to all our archives.