Crystal Clear: An Interview with Shea Zellweger

In 1953, while working a hotel switchboard, a college 
graduate named Shea Zellweger began a journey of wonder and obsession that would eventually lead to the invention 
of a radically new notation for logic. From a basement in Ohio, guided literally by his dreams and his innate love of
 pattern, Zellweger developed an extraordinary visual 
system—called the “Logic Alphabet”—in which a group 
of specially designed letter-shapes can be manipulated like puzzles to reveal the geometric patterns underpinning logic. Indeed, Zellweger has built a series of physical models of his alphabet that recall the educational teaching toys, or “gifts,” of Friedrich Fröbel, the great nineteenth-century founder of the Kindergarten movement. Just as Fröbel was deeply influenced by the study of crystal structures, which he believed could serve as the foundation for an entire educational framework, so Zellweger’s Logic Alphabet is based on a crystal-like arrangement of its elements. Thus, where the traditional approach to logic is purely abstract, Zellweger’s is geometric, making it amenable to visual play.

Like his notation, Zellweger’s working methods are delightfully unconventional. While constituting 
a genuine research project in logic, his notebooks 
(made between 1953 and 1975) have remarkable visual appeal, passing through phases reminiscent of Russian 
Constructivism, outsider art, concrete poetry, and pop. These days we accept outsider artists, and are perhaps aware of outsider scientists, but Zellweger may be the first we could define as an outsider logician. Although he has worked on the Logic Alphabet for over fifty years, his professional life has not been spent in departments of philosophy or mathematics, but in psychology, mostly at Mount Union College in Ohio, from which he retired in 1993. After half a century of obscurity, Zellweger’s work is starting to attract the attention of some mathematicians who believe it offers an exciting new perspective on logic. Christine Wertheim, co-director of the Institute For Figuring, has been studying Zellweger’s work, and talked with him about his unorthodox approach.


---

Christine Wertheim: The history of logic is very interesting, and has undergone many phases. In the Western world, it began about 2,500 years ago when the Greeks were developing a new form of civic structure in which debate and argumentation replaced allegiance to tradition as the major political tools. Slowly philosophers realized that, if laws were to be based on the outcome of arguments, an understanding of how valid 
arguments are actually constructed was crucial. Formal logic began when thinkers such as Aristotle started using simple diagrams, like the famous Logic Square, to study these structures. This was an amazing innovation which applied a mixture of algebra and geometry to the study of language, that is, language in its role as the medium of argumentation. During the Middle Ages, many thinkers dreamed of making a complete mathematical analysis of logic, a complete formal notation for describing arguments and their components. The Spanish nobleman Raymond Lull, a famous eleventh-century debaucher who later turned religious, was probably the first to have the idea, and in that sense he is considered by some as the great-great-grandfather of computing. However, the mathematization of logic did not get very far practically until the mid-nineteenth century when an Englishman named George Boole developed the first fully-fledged formal notation. The study of logic radically changed at this point. It’s not dissimilar to the way that sixteenth- and seventeenth-century physicists revolutionized the study of motion by mathematizing it. In what way does your work relate to this innovation?

Shea Zellweger: Since Boole’s groundbreaking work, most logicians have looked to algebra for models of how to formalize logic, which is why it’s now so abstract. But logic can also be modelled as a geometric system, and when you do this you get quite a different view because you see that it’s not just a set of abstract symbols but is composed of a fascinating group of symmetric patterns. These patterns are the basis for my Logic Alphabet.

So that we can compare what you’ve done with the standard notations, can you give a layman’s description of how logic is thought of today?

Let me make an analogy with arithmetic. In arithmetic we
construct equations by combining numbers through operations such as addition, subtraction, multiplication, and division, symbolized by the signs +, –, x, and ÷. In logic you don’t combine numbers, but propositions such as “cats have four legs” or “trees have leaves,” which are symbolized by letters such as A, B, C, and so on. Just as numbers can be manipulated using arithmetic operations, so propositions can be manipulated by combining them through logical operators called connectives. The most common connectives are “and,” “or,” and “if…then…,” which each have their own symbols. With these you can write such logical expressions as: [ (If A then B) and A ]. Then, just as in math you can use the laws of arithmetic to find the solutions to equations by reducing them to a simple value—for instance, the solution to the equation [ ((2+7) x 8)) ÷ (3 x 2) ] is 12—so there are laws that enable us to find solutions to logical expressions. The “solution” to the example cited above is “B.” This might seem very trivial, but modern computers are built around these kinds of operations. A computer is really just a great big logic-processing machine.

But in standard logic there are symbols for only 
three or four of the connectives. Yours has sixteen. Why so many?

It’s much like the difference between the Arabic and Roman numeral systems. The Romans had distinct symbols for 1, 5 and 10, that is, “I,” “V,” and “X,” and for the higher numbers they added “L” for 50, “C” for 100, “D” for 500, and “M” for 1000. All other numerals were constructed from combinations of this idiosyncratic set. This means that the number “VIII” can’t be interpreted by the place-based method we’re familiar with—which would give 5,111. Instead you have to see it as a sort of mini-equation that reads “5+1+1+1,” i.e., 8. In this way Roman numerals were an ad hoc mixture of number-values and equations.

What’s different about the Arabic system?

The Arabs (with help from India) settled on a consistent 
use of base ten, gave each number within this base its 
own symbol (the numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, 9), and then imposed a macrostructure in which the units, tens, hundreds, and thousands were each given their own distinct columns or places. With this system you can more easily do arithmetic and uncover the patterns inherent in numbers.

Is your Logic Alphabet analogous to the Arabic numerals?

That’s right. The standard notations are analogous to the Roman numerals and mine is like the Arabic system, because there are sixteen logical connectives in all, but 
most notations only use three or four, cobbling the others together from combinations of these few. In my notation, 
all sixteen are given equal prominence, and each has its 
own symbol, just as each of the units in the base-ten Arabic system has its own symbol.

And it’s because you use all sixteen that your notation shows the geometry and symmetries underpinning logic?

Yes, you only see the symmetric patterns in the system when you look at the whole thing with all sixteen elements together. When you use only a few, you don’t see the beautiful crystalline structures. My notation is designed to highlight these wonderful patterns, not obscure them, as most notations do.

But why do you need to show these patterns? Both people and computers are doing fine using only three or four 
connective symbols, and not having a clue about the lovely 
patterns hidden below. Why do you think it’s so important to reveal these?

It’s a bit like cladding a house in glass so you can see how it’s actually built, rather than covering it all in plywood and stucco, which hide the underlying structure. To me, it’s important not to just be able to do something, like driving a car. I also want to know how the thing works. In my notation, you could say that the design puts what’s under the hood onto the dashboard, so you learn how the vehicle works while you’re actually driving it. This makes the whole act of driving much less passive, and ultimately much more satisfying. I also like the fact that one’s interaction with my notation is literally hands-on and physical, rather than just all in your head. Knowledge shouldn’t be disconnected from the body. The body should be used as much as possible as a part of the means through which we acquire and store knowledge. Why can’t logic be like that too?

Does this mean that your notation offers not just a new kind of logical notation, but a whole different mindset—a new perspective, really, on what logic is?

It is a different mindset, but what’s really important is how this approach plays out in the teaching of logic. For most people, if they have encountered logic at all, it has probably seemed complicated, difficult, and full of abstract rules and symbols. My system is like a game whose simple and explicitly exposed structures enable you to easily understand the basic principles of logic, and even to begin doing some elementary constructions without learning any complicated rules. This is because the geometrical model on which it’s based can easily be embodied in objects you can manipulate with your hands and eyes. In fact, you can just play with the system as an interesting set of patterns in its own right. By flipping and rotating the elements, you can explore the symmetries embedded in the system without seeing it as a way of modeling logic.

Your notation is specifically designed then to make these symmetry patterns tangible?

The Logic Alphabet is a very special kind of writing that uses sixteen letter-shaped symbols whose forms have been carefully designed to mimic the geometrical patterns underpinning logic. In many ways, it’s more like a pictographic language than a phonetic or purely abstract one. However, the pictorial aspect doesn’t just lie in the shapes of the individual symbols, but also in the relations between them. What is important is the way you can turn one letter-shape into another by flipping and rotating, and that you can literally see this when you do it.

Can you give me an example?

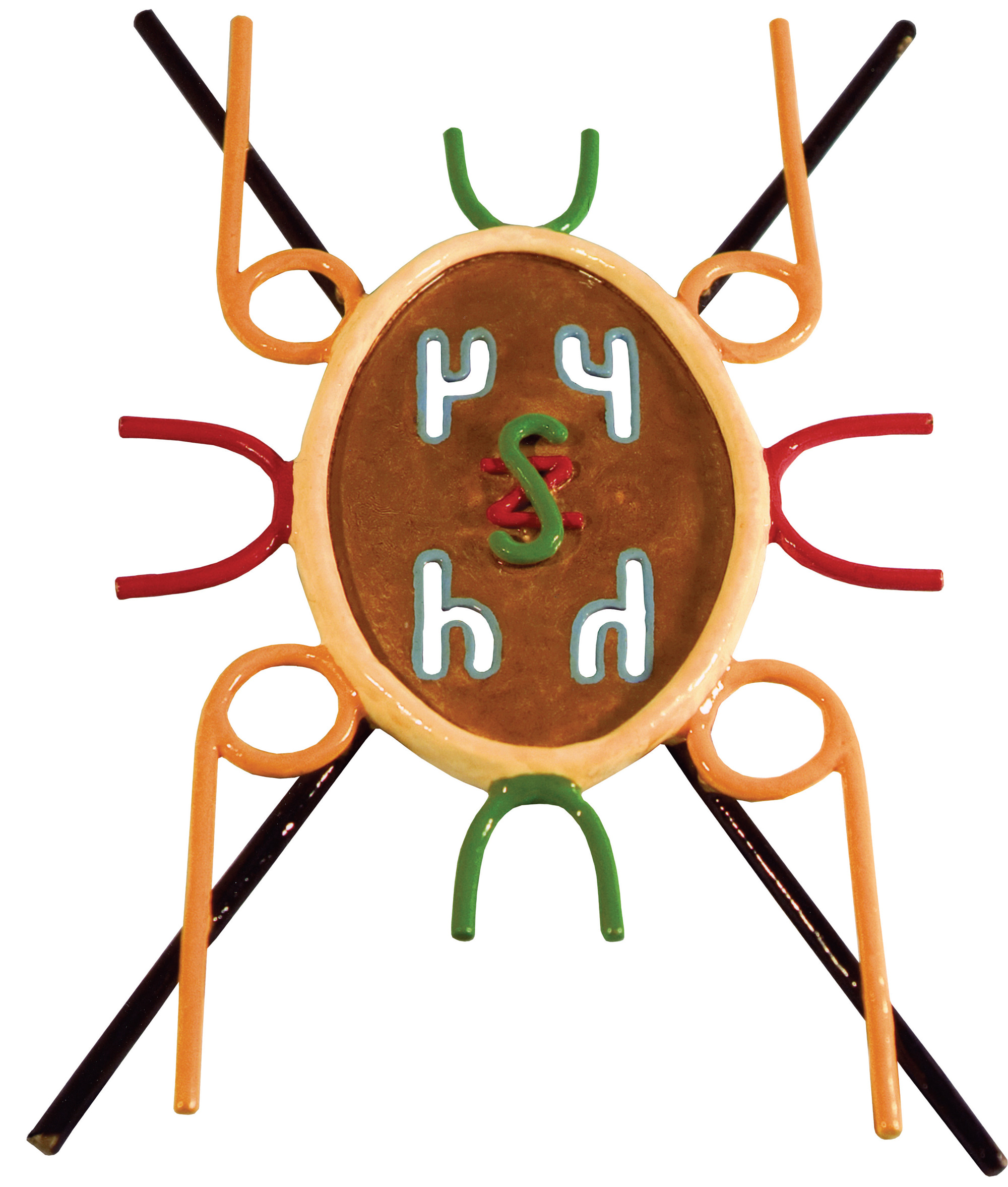
For instance the Logic Alphabet includes the symbols “d,” “b,” “q,” and “p.” If you flip the d-letter to the right, it turns into a “b.” If you flip it upside-down it turns into a “q.” If you do both together, it rotates into a “p.” The other symbols in my Alphabet are also related by very specific symmetries which can be described by flips and rotations, and together all sixteen form a pattern you can have great fun with. But it’s easier to grasp if you look at a three-dimensional model first.

You built some models specifically for this purpose, didn’t you?

Yes. The Logic Alphabet is a script designed to be written on paper, so it’s only in two dimensions, but the overall patterns it captures are actually in four dimensions. Of course, we can’t build anything in four dimensions, but there is a three-dimensional version that neatly encapsulates the basic figures. In the 1970s, I built some models as teaching tools, which beginners can play with. In this way they become familiar with the symmetries and beautiful patterns, long before they are able to think about logic itself.

In this sense your whole approach is similar to the ideas developed by the great nineteenth- and early twentieth-
century pedagogues Friedrich Fröbel and Maria Montessori, who founded the Kindergarten movement and the Montessori school system, respectively. Both believed that higher-level conceptual thought should be preceded by concrete hands-on play with geometric forms embodied in solid materials.

That’s right. The whole way logic is taught today, as a system of purely abstract signs that only college-level students can understand, is completely backward. The Fröbel-Montessori method of acquainting children first with fundamental patterns, and then later putting letters and other symbols on these to show how the same forms are embodied in natural phenomena and geometric figures, is exactly right. I’ve just extended this methodology to logic. In fact, I think of myself as a Fröbelian logician rather than as an outsider, because I think of logical structures as figures of thought, figures that can be explored materially.

You said that the patterns underlying logic have a crystalline structure, and that it is the symmetries of this crystal that your notation allows us to see and play with. Can you explain this?

As I said when talking about the models, the Logic Alphabet is like a two-dimensional presentation of a higher-dimensional figure. The three-dimensional version of this figure is a rhombic dodecahedron, which is formed by the inter-penetration of a cube and an octahedron. I call it the Logical Garnet because it looks like the gemstone garnet. The 
letter-shapes of the Logic Alphabet were specially designed to make the symmetries embodied in this figure as easy to see as possible, and as easy to manipulate.

We don’t normally think of mathematical and logic notations as works of “design.” We mostly assume that when a new symbol is needed, someone just makes it up without much thought about its aesthetic qualities. At least, that’s what I thought until I saw your work.

We take the Arabic idea of one numeral for each unit within the base for granted, but it was a profoundly creative act. Many other cultures had usable ways of symbolizing 
numbers, but none of them were as powerful as the Arabic invention. Once you realize that the logical connectives form a group of symmetry relations, you are almost inevitably 
led to the idea that these should be reflected in the shapes of the symbols themselves. This is what’s missing in the standard notations.

In the Logic Alphabet, all sixteen connectives have their own names, and each has a letter-shape as its symbol. I believe you’ve devised a mnemonic to remember them by?

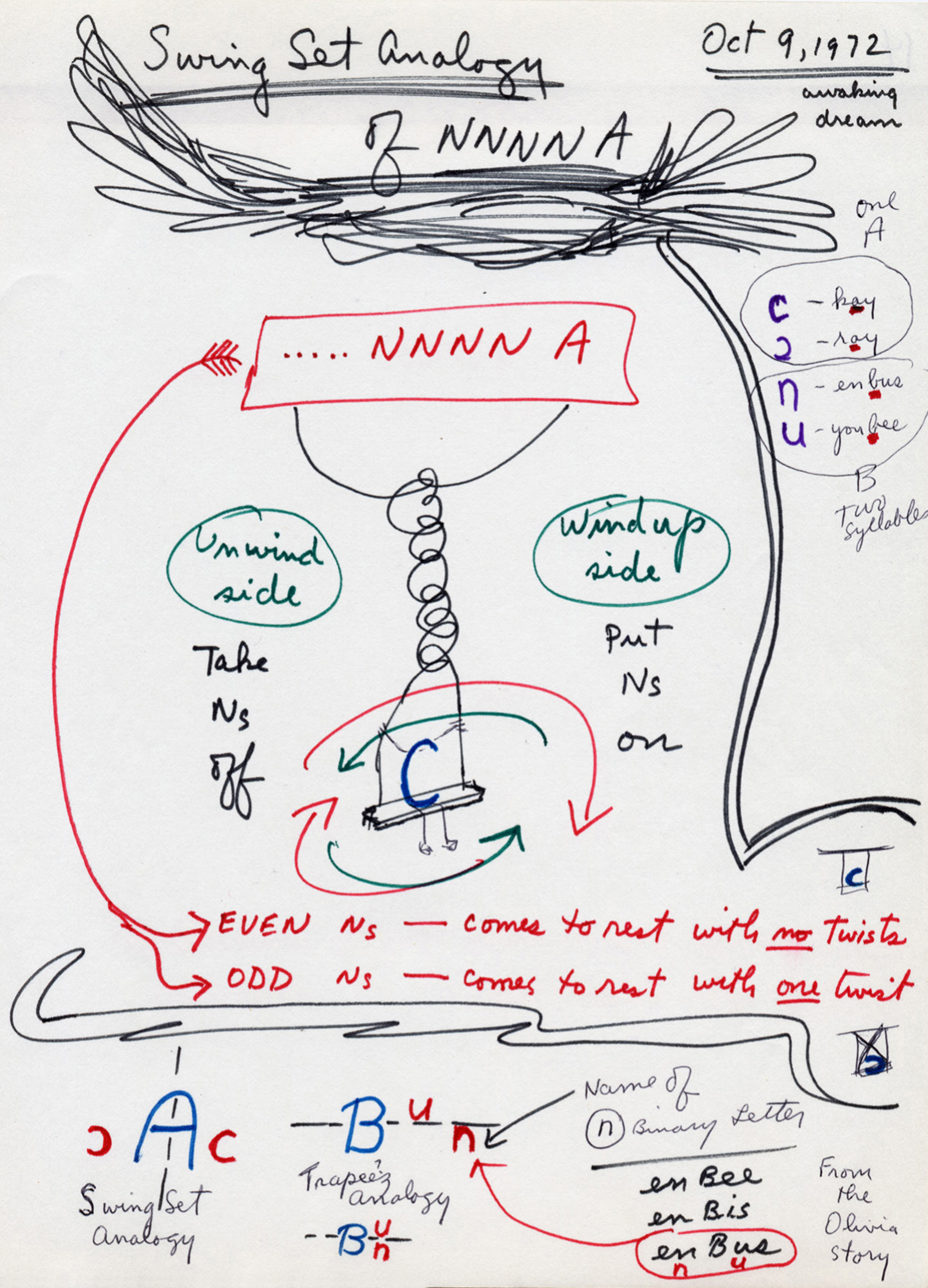
Yes, I call it the Olivia Story:

It’s a mini-drama with sixteen letters and five acts about a man who keeps being interrupted by his daughter’s noisy play. At first he tries gently to persuade her to desist. When this fails he becomes increasingly exasperated, and winds up ordering her out of the room altogether, or leaving himself! I had to make up my own pronunciations for the words beginning with the four nonstandard letters—rackett, mifty, riftee, yorders—hence the increasing sense of chaos and linguistic breakdown as the narrative unfolds.

You have said that dreams played a part in your logical research. Could you explain this?

I’ve worked on this project a long time, so my mind keeps thinking about it, even when I’m doing other things. I never know when an idea will resolve itself, and when it does it can be at the oddest times, like in a faculty meeting. Once I woke up from a dream with an image of the letter “c” on a swing spinning round and round. It gave me the solution to a problem I was occupied with at the time.

You seem to have mostly been working alone...

I don’t feel that I’ve ever really been alone. I have worked outside the fields of professional logic. 
I never taught it, nor even enrolled formally in any classes. I’ve pursued this thing in my spare time, and on occasional sabbaticals, but I was always able to find “soft spots,” generous mathematicians who would from time to time listen to my ideas and give me help, especially the great geometer H. S. M. Coxeter, and my faculty colleague Glenn Clark.

In the 1970s, you took out patents on your ideas. Why did you do that?

It was really an end run. Up to the mid-1970s my papers always came back with rejection slips. So when I started making the models, I figured that a record of my diagrams in the patent office would be at least one place where my work could be anchored publicly. You can’t patent ideas, such as logarithms, but you can get a patent on a slide rule, which is a material embodiment of them. My first patent was filed in October 1976, but not granted until June 1981. It was a long and torturous process. You have no idea!

Was it worth all the trouble?

Absolutely. The specification included in each patent notes that my models are an “introduction to the crystallography of logic.” That was the first time that this expression, which links logic to its deep roots in symmetry, was used in print.

I believe your work is finally receiving some attention in the logical arena.

No, it isn’t. Logicians aren’t interested at all. Unless you speak in their language, they don’t want to know about your work. However, there are a few mathematicians who have taken an interest. You can find references to their papers on my website at www.logic-alphabet.net.

Given how entrenched the logic world already is in its current notations, do you think your system, or something like it, will ever take off?

Something like it, a notation of the same geometrical type as the Logic Alphabet. Yes, absolutely. I think it is inevitable. This is Fröbel, Montessori, and Piaget all over again. Just give one generation of children the hands-on opportunity to play with models like mine in the early years of their cognitive development, and it could transform the way we do logic.

­