Menger’s Spongiform Encephalopathy
Building a fractal house of cards
Margaret Wertheim and Jeannine Mosely
Menger’s Sponge—named for its inventor Karl Menger and sometimes wrongly called Sierpinski’s Sponge—was the first three-dimensional fractal that mathematicians became aware of. In 1995, Dr. Jeannine Mosely, a software engineer, set out to build a level three Menger Sponge from business cards. After nine years of effort, involving hundreds of origamists all over America, the Business Card Menger Sponge was completed. The resulting object is comprised of 66,048 cards folded into 8,000 interlinked sub-cubes, with the entire surface paneled to reveal the level one and level two fractal iterations. The classical Menger Sponge is constructed in three dimensions, but analogous objects can be embodied in any number of higher dimensions, and, according to theories of loop quantum gravity, the structure of spacetime may be allied with this foam-like form.
As one of the pioneers in the emerging field of computational origami, Mosely is an expert on the subfields of business card origami and minimalist origami, in which one is restricted to no more than four folds. She also conducts research on curved crease origami, exploring the potentialities of non-linear foldings. Moseley was trained as an electrical engineer at MIT and has worked in the computer-aided design (CAD) industry writing three-dimensional modeling software. In August 2006, the Business Card Menger Sponge was exhibited by the Institute For Figuring at Machine Project gallery in Los Angeles. IFF Director and exhibition curator, Margaret Wertheim, talked with Mosely on the eve of the show.
Margaret Wertheim: It’s a pretty quixotic project: How did you come to be doing this?
Jeannine Mosely: I’ve been doing origami most of my life. And in the 1980s, I got interested in modular origami, where you make lots of units that are all the same, called “modules,” and link them together to make something bigger and more complicated. I had learned a traditional modular design—an interesting little design for making cubes—and I showed it to a lot of people and they said, “Oh, that’s cute.” But then one day, I realized it was possible to link the cubes together and so you could go from having a module to a meta-module that can be linked to make even larger structures. I began to think about what kinds of shapes I could build with those modules—what would be interesting to make with a lot of these cubes? I’d also been interested in fractals and I thought about the Menger Sponge, and I thought it might be fun to try to make one out of those cubes.
How would you describe this particular fractal?
There are two ways of thinking about it: one of them is additive and the other is subtractive. In the subtractive model, you start with a cube and let’s imagine that you subdivide it into a block of twenty-seven smaller cubes. That is, you divide the original cube into thirds in each direction, so it becomes a block of three by three by three little cubes. You then remove the little cube at the center of each face and also the one in the center of the whole block, so that you are taking away seven of the little cubes, leaving twenty in place. What you are left with is something that looks like your starting cube with a square hole drilled through each major axis, and so it creates an open framework. That’s what I call a level one Sponge. You can repeat this whole process with each of the twenty remaining cubes. At the end of that you’ll be left with 400 even smaller cubes, to get what I call a level two Sponge. Repeating that process again, you go to 8,000 even tinier cubes. If you keep on drilling down and down, you get to these smaller and smaller units until there is essentially nothing left—and that’s the Menger Sponge.
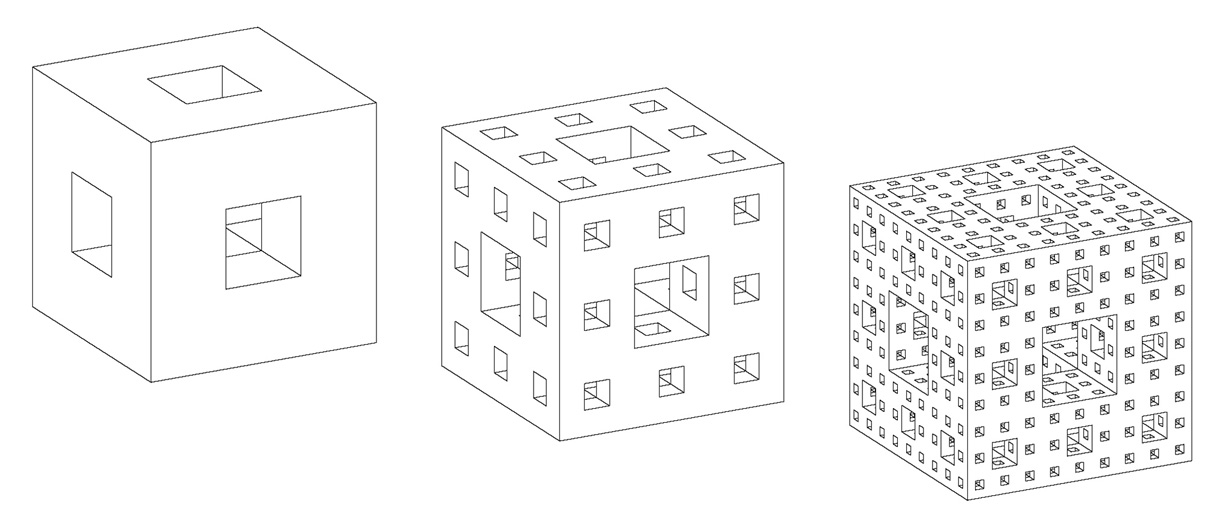
The other way of looking at it—which is how I actually built my Sponge—is the additive view. Here you start with twenty small cubes and build them up to a structure that looks like the cube I described above with the square holes drilled in it. It’s got eight of the little cubes in each of the corners and twelve along the edges connecting the corners—that’s a level one. You make twenty of these level ones and connect them together in the same pattern to make a level two (that’s 400 of the smallest cube units). Then, to make a level three Sponge, you make twenty level twos and link them together, so now you have twenty by twenty by twenty cubes. If you can keep on going, it just grows and grows.
What are the properties that make something like this a fractal?
There isn’t a strict mathematical definition, but there are a number of properties fractals share. One of them is that it should be self-similar. What this means is that when you zoom in on one little spot, it should look exactly like the larger structure of the whole thing. A good simple example of a fractal is the Cantor Set, which is a famous mathematical object that’s closely related to the Menger Sponge. It’s named after the mathematician Georg Cantor, who discovered it—but here instead of starting with a cube and subtracting little cubes, you start with a line segment and remove the center third of it. Then you keep on removing the center third from each of the remaining two pieces, and so on and so on. The resulting form is a type of “fractal dust,” and no matter how closely you look at it, every little part of it exactly mimics the whole structure. It’s actually a one-dimensional version of the Menger Sponge.
Historically speaking, fractals were a radical mathematical concept that was only understood in the very late nineteenth and early twentieth centuries. What was so important about the discovery of these objects?
Well, it led mathematicians to questions about the concept of measure. There’s an entire theory called Measure Theory, related to measuring things. How big is something? We all have a kind of intuitive understanding of measuring things—you can plot a ruler to see how long something is or you can use a ruler in two dimensions to find out the area, or in three dimensions to find out volume. But with objects like the Cantor Set and the Menger Sponge, with lots of infinitesimal pieces, it’s difficult to measure them. They have strange properties, and when mathematicians tried to measure them, they discovered some interesting things.
One of the strange properties is that fractals don’t have a discrete dimensionality—that is to say, they are not clearly one-dimensional or two-dimensional or three-dimensional, like most objects we are familiar with, but have something in between. What does it mean to have a fractional dimension?
In some sense, a Menger Sponge is a three-dimensional object. Clearly it exists in a three-dimensional space. But when you try to measure its volume, it turns out that it has no volume at all so it can’t be a fully three-dimensional thing. This is a difficult concept to explain. One way of understanding it goes like this: suppose we draw a line and we measure it with a ruler and it’s one foot long. Suppose now that we expand our line by a factor of three—so we have a line that is three feet long. Imagine now that we draw a square with each side being one foot, so it has an area that’s one square foot. If we expand the square by a factor of three so that we have a square that measures three feet on each side, it has an area of nine square feet—that’s three squared. Imagine now that we draw a cube, whose sides are each one foot. This time, if we expand in all directions by a factor of three, we get a volume that is twenty-seven cubic feet—that’s three cubed. From this, we discovered that with the line, its measure increased by three to the first power; with the square, its measure grew by three to the power of two, because the square is two-dimensional; and when we expanded our cube, it grew by a factor of three cubed, because it’s a three-dimensional object. But if you look at the Menger Sponge, what you see is that each time you expand it by a factor of three, its volume only goes up by a factor of twenty—not by twenty-seven, as we would expect with a normal cube. So we can define a kind of fractional dimension here which is more than two but not quite three. In fact for the Menger Sponge, its dimension is 2.7268 (there’s actually an infinite number of decimal places here).

The Sponge has no volume, so in some sense it is actually a linear object. Menger proved that it is the “universal curve,” which means that all possible curves are embedded in it. So does that mean my name is written somewhere in there?
I’ve never really thought about that, but I guess that’s right.
I’d like to come back to how you built your Sponge. Why did you decide to make it out of business cards?
The design for the basic cube module I used is pretty old. When I learned how to make it, someone suggested I use playing cards. But, I didn’t have any playing cards I wanted to ruin and I looked around my desk and saw a box of old business cards I wasn’t using. So I started folding with them. After I had been folding for a while, I came up with my own designs, not just for a cube, but a great many other things, and so people kept giving me their old business cards. Then the company I worked for changed its name and I got everyone’s old business cards. I began to have a ridiculous amount of cards laying about—around 50,000—and people were teasing me about what I was going to do with all these business cards. So I made a little joke that maybe I’d make a big Menger Sponge—a level three Menger Sponge. I was really kind of kidding at first. I didn’t know if it would be possible, because I didn’t know how long it would take and I didn’t know if it could bear its own weight. And so these were questions I had to answer before I could even proceed with the project.
You’re an engineer. Once you had the idea, did you sit down and do a lot of calculations about whether it was possible and what it might take?
Oh yes. I had conversations on the Internet with friends who were also origamists and I did a lot of calculations. I also did some early structural tests. One thing was that I made a cube and stacked one-pound weights on it, to see how much weight a cube could bear before it collapsed. It turns out that a box of standard American business cards weighs about a pound (roughly half a kilogram) and, surprisingly, a business card cube can carry close to a ten-pound load. I calculated the number of cards I needed and I determined that a level three business card Sponge would weigh 160 pounds. That is distributed over 8,000 cubes. Some cubes bear a heavier load than others, but none of them was going to bear a load of more than a couple of pounds, so I was pretty sure it was going to hold up under its own weight.
Another calculation that was important was how big would this thing be? American business cards measure 2 x 3.5 inches, so when you make a cube out of them, the cubes are 2 inches on each side. A level one Sponge is three by three by three cubes, so it’s only six inches on each side. A level two Sponge is three times as big, so it’s eighteen inches on each side. A level three Sponge is fifty-four inches on a side—though not outrageous, that’s getting pretty big. It was apparent that it was not going to fit through a doorway and that was a problem, because either I needed a space where I could build it and it could stay there permanently, or I needed to find a way to build it in pieces so it could be moved from place to place.
That’s the option you chose. And that required a whole other set of logistical challenges about how to decompose it into pieces that could easily be moved and assembled. Can you tell us about that process?
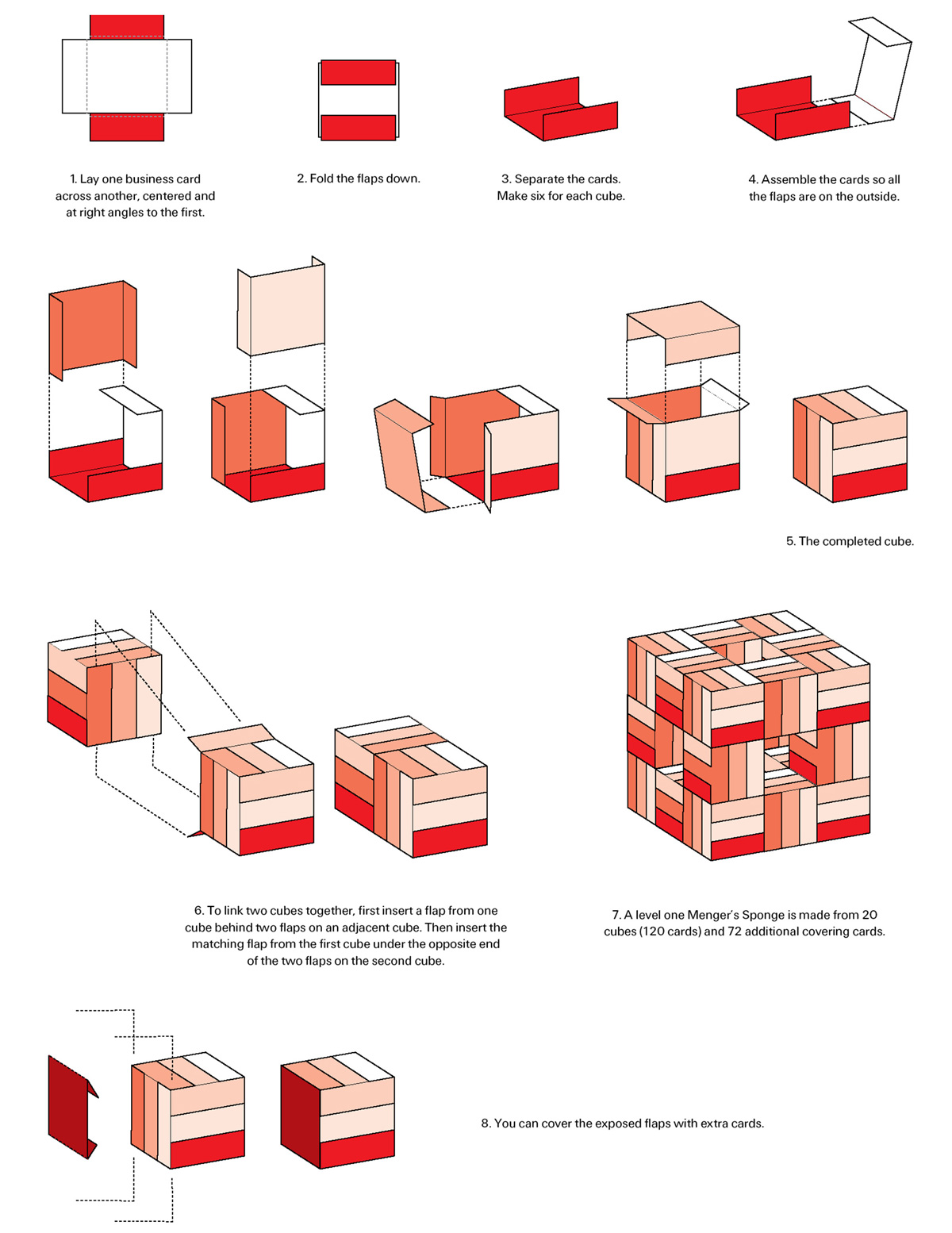
At first glance, it seems that the obvious thing to do would just be to build 400 level one Sponges or twenty level two Sponges and then link them together. But it turns out that won’t work. The way you link the individual little cubes together is that each cube has flaps on its surface that have to be hooked under the flaps of adjacent cubes. When you take two level one Sponges and try to link them together, you would need to be able to get at all these flaps and it isn’t possible mechanically. So you just can’t build a bunch of smaller Sponges and link them together. Instead, I had to come up with a whole different way of decomposing the Sponge into subunits that I call Tripods. These can then be assembled together into groups that can in turn be assembled into the whole Sponge. It’s actually pretty complicated, and working this out was one of the more tricky parts.
Did you calculate all that before you started building, or did you only realize that you’d have to do this subdivision once you got into it?
I worked all this out in advance. I used software to help me with some of the calculations and I made computer models as well. One of the reasons I did it this way was that I wanted to build it as a community project. I wanted to involve other people and teach them about origami and fractals and engineering and mathematics. So I wanted to be able to break it up into smaller pieces that other people could build. Because of that, it was necessary to work out the details of exactly where every tripod would be located in the final Sponge. There are 448 tripod module groups in all, and I had to give very explicit instructions to my volunteers to make sure that all these pieces would fit together properly.
What kind of people contributed?
I gave classes for several years at MIT in what they call the independent activities period. I also lectured on the Sponge to a group that would meet regularly at Harvard called the Philomorphs. They were a group that liked to get together and talk about shapes. All these people contributed cubes. I also taught classes at origami conventions like Origami USA, and in schools, mostly in the Boston area where I live, and in Charlotte, North Carolina, in association with the South East Origami Festival. Children and origamists in those places also contributed cubes. Then there’s a conference that’s held every couple of years called the Gathering for Gardner in honor of Martin Gardner, a very important recreational mathematician who wrote a column for Scientific American for many years. Some of the world’s greatest mathematicians attend—I taught a class there once and I collected cubes from some really brilliant minds and incorporated them into the Sponge as well.
I worked on this project for close to ten years, and, frankly, one of the reasons it took so long was because it was a community project. If I’d decided to build it alone in my garage, I could have built it much quicker!
Now you’ve built a level three Sponge, would you consider doing a level four?
I’ve thought quite a bit about the level four Sponge and there are a number of technical problems. If I were to try to make one, it would need more than a million business cards and it would measure fourteen feet on each side. But the biggest problem with a level four Sponge is that it would weigh a ton and a half and it probably would not support its own weight. I’ve done the calculations and the load on the cubes in the middle plane would be too great.
So the one you’ve made is the biggest business card Sponge we could hope to realize—it’s the apex of physical possibility?
I think so.
You’ve put in many thousands of hours into this project over almost a decade. Some people might see that as a form of madness.
Yes, I have to say it has been a long process. My husband Allan is a wicked punster and he told me early on that I was suffering from Mad Card Disease, which is known scientifically as Menger’s Spongiform Encephalopathy! My family has been amazingly supportive.
So is it a form of madness?
I guess I would like to point out that lots of people have done similar things—people who have woven an oriental rug or a tapestry, or crocheted an afghan, or made a complex needlepoint project. Many people do things like this and sometimes it’s the joy of working with your hands and sometimes it’s the joy of seeing things grow and watching the structure unfold in front of you. The Sponge doesn’t actually unfold, but in a way, it does. As I fold it, the interior takes on amazing strange symmetries that only the person who builds it really has the privilege of seeing. Then there is the issue that as it grew, I also felt a responsibility to all the volunteers who’d contributed. If I felt discouraged and thought “Why bother?,” I’d look at it and say, “What are you going to do with it? Throw it out? What are you going to say to all those people who helped?” Once you start something like this and you get other people involved, you have a responsibility to finish it. And now that I have and I’ve seen what it looks like, I’m really glad because it’s an amazing object—more amazing than I thought it would be.
See press about “Menger’s Spongiform Encephalopathy” on Scientific American’s Roots of Unity blog.
Jeannine Mosely is an electrical engineer, computer scientist, and computational origamist based in Boston.
Margaret Wertheim is founder and director of the Institute For Figuring, a Los Angeles-based organization dedicated to the aesthetic and poetic dimensions of science and mathematics. She is currently working on a book about outsider physics and the role of imagination in theoretical science.
Spotted an error? Email us at corrections at cabinetmagazine dot org.
If you’ve enjoyed the free articles that we offer on our site, please consider subscribing to our nonprofit magazine. You get twelve online issues and unlimited access to all our archives.