The Fax Numbers of the Beast, and Other Mathematical Sports: An Interview with Neil Sloane
The online encyclopedia of integer sequences
Margaret Wertheim and Neil Sloane
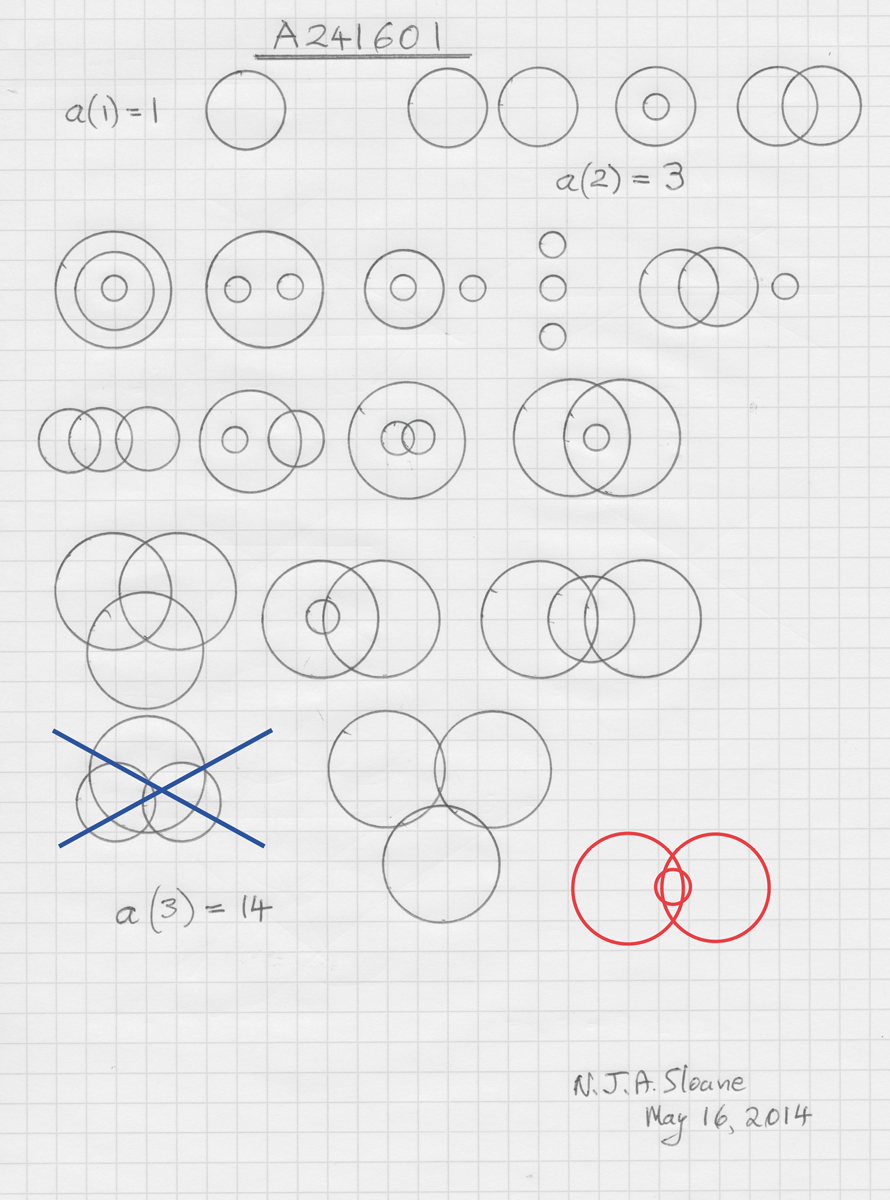
Everyone knows a few integer sequences: the even numbers, the odd numbers, the primes. And we’ve all heard about the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13…), where each term is computed by adding together the two previous terms. In 1964, mathematician Neil Sloane, then working on a PhD at Cornell University, began to write down interesting sequences of numbers on file cards. His research on neural networks generated quite a few; he pressed his friends for examples and consulted mathematics textbooks. As the horde of sequences grew, he transferred them to punched cards, then magnetic tape, and eventually to the web, where today, more than half a century later, his Online Encyclopedia of Integer Sequences (OEIS) has surpassed 250,000 entries. Used widely by professional mathematicians, computer theorists, and scientists, the OEIS has been called the most influential math website in the world. In addition, the database draws a huge international audience of recreational mathematicians, people who, for pleasure, surf its delights to explore the ways in which numbers can play. As a kind of numerological version of the Oxford English Dictionary, the OEIS is the place to go if you want to learn what any sequence of digits might mean, if it has been discovered already, or if it is entirely new. Every entry has a formal catalogue number and is complete with technical definitions, links to a vast network of citations and references, a visualization of the sequence as a graph (oftentimes revealing elegant patterns), and the option to hear it played as a piece of music. In February, Margaret Wertheim spoke by phone to Sloane, who runs the OEIS Foundation in Highland Park, New Jersey.
Cabinet: What compelled you to begin the OEIS?
Neil Sloane: Of course, it wasn’t called the OEIS in 1964. O stands for “online” and that didn’t happen until 1996. At the beginning, I called it a Dictionary of Integer Sequences, and in 1973, I published a small handbook that had 2,373 sequences. When I got to 10,000, I decided to put it on the Internet.
Originally the idea came from work I was doing for my PhD thesis at Cornell. I was studying neural networks, which are like artificial brains with computer simulations of neurons. When these “neurons” fire, they trigger other neurons, which in turn trigger others—you have to have a certain amount of activity before a neuron gets triggered. And the question was, “If you have a network of these configured in a particular way, and you start by making one fire, will the activity continue to propagate through the network? Will it die out, or will it saturate the network?” I was looking at models of this, and I could count the number of cells firing at any given time, and I would come up with a sequence of numbers. For instance, if you start with one neuron firing, that might trigger two others that in turn trigger six, then twenty, and so on. Then after a while, the firing might die out. So using a computer, or by hand, I could calculate the beginning of a sequence, with each configuration of the network having its own specific sequence.
I knew I was going to have a lot of sequences I needed to understand. The first one I looked at, I couldn’t find in any of the books. I looked in the obvious places: John Riordan’s book on combinatorial analysis, Abramowitz and Stegun’s Handbook of Mathematical Functions, and others. There were lots of sequences there, but not the one I had. So I thought it might be helpful to make a list of sequences I came across, in my own work and also in math books and journals. I started writing them on file cards and it seemed no one had done this before. So I started the collection and it began to grow.
Do you still have the file cards?
Oh, no. I threw them away years ago when I transferred it all to punched cards. That was in the late 1960s, shortly after I joined Bell Labs. In the early 1970s, I transferred the collection to magnetic tape. I don’t have the punched cards or tape either. It’s all on the network these days, up in the cloud. I’ve been doing this for fifty years and as computers have progressed, every step forward has made my life easier.
How do mathematicians benefit from this database?
If you’re a writer and you want to know how a word is used, you can look it up in the Oxford English Dictionary and find the record of the first person to use the word and examples of how it is used in a sentence. Well, it’s the same thing with integer sequences. You come across a sequence in your work and you want to know, “Am I the first person to see this sequence, or has it been studied before?” Until my database, there was nowhere you could find that information, so it’s been a great boon to mathematicians. They can look up a sequence and say, “Oh, that’s something that came up in topology in the 1940s.” Or, “This was a sequence that came up in chemistry in 1929.” It will tell you things you didn’t know about your sequence, such as, “This is also the list of the number of nodes in labeled, rooted trees.” And your context might be totally different. So if my database tells you this comes up in studying the periodic table or in counting the branches in binary trees, that’s very interesting to you, especially if I give you a formula or computer program so you can compute a lot more terms of your sequence.
It’s also great fun. There are a huge number of recreational mathematicians—people who just love numbers—and they will browse the database looking for interesting sequences. And some will try to create new or interesting sequences themselves. So there is a lot of pleasure. It’s like going to a museum or a gallery and looking at the latest artworks.
What makes for an interesting sequence?
What makes for a good painting, or a good piece of music? It’s the same question. The editor has to decide. I have a board of editors, a large group of people who are hard at work all the time, night and day all over the world, looking at submissions and deciding whether or not they are worth putting into the OEIS. If one of them says, “Yes, this is great,” then it goes in. Or, one will say, “This is junk. This does not belong in the OEIS.”
How do you determine “junk” in this context?
As an example, one person tried to submit the sequence giving the number of pages in each of the seven Harry Potter books. That is not something we accepted because, first of all, it depends on the edition. Are we talking about the paperback edition, the hard cover, the English edition, the American edition, the German translation? And so on. Do you include the front matter, or the stuff at the back? What do you mean by the number of pages? It’s not a well-defined problem. This is a scientific database, and if I’m going to make an exception about accepting non-mathematical sequences, then it had better be something people have discussed.
For instance, subway stops in Manhattan. There are several different New York City subway lines with stops at numbered streets (14th Street, 23rd Street, 34th Street, 42nd Street, etc.), and these are famous sequences. They come up in IQ tests all the time, so they go in, no question. Or the sequence of numbers around a dartboard. There are only two or three different conventions for dartboards, so they go in; and the numbers around a roulette wheel. These are non-mathematical, but they’re interesting, and in my judgment deserve to be in the OEIS.
So it isn’t just pure mathematics?
No. There’s chemistry, physics, biology, botany, and many other things, including cultural sequences. I would regard a dartboard as a significant cultural sequence. We also include the list of years in which the eighteen King Louis of France came to the throne. Maybe this one is questionable, but I accepted it at the time. Marginal sequences having to do with dates involving, say, American politicians, those usually don’t seem well defined. Things that depend on the calendar year—like the dates of Easter—some get accepted, others rejected.

If I’ve got a sequence of numbers from some cultural or physical domain, can I submit it for consideration?
Yes. Anyone who registers and gives a real name can submit sequences. We have thousands of people submitting from all over the world.
This parallels the making of the Oxford English Dictionary chronicled in Simon Winchester’s book The Professor and the Madman, where people all over the planet contributed word entries that were vetted by professional philologists. What kinds of people submit integer sequences?
There’s a wide spectrum: mathematicians, and also a lot of computer scientists who are typically counting the number of steps needed to carry out some sort of procedure, such as sorting a long list of words. The study of the complexity of various algorithms is a major part of computer science and these studies tend to come up with sequences of numbers. For example, if you’ve got a particular sorting algorithm—say you want to arrange playing cards in ascending order—what’s the worst-case number of steps it would take if you have to sort five cards, six cards, seven cards, and so on. There are also people who aren’t mathematicians, but may be professionals in some other field, who send in sequences they’ve come across in their work. And then there are a lot of amateurs.
Mathematics as a field encompasses a great deal of play. One thinks of Martin Gardner’s wildly popular “Mathematical Games” column in Scientific American. I’m fascinated by the notion of amateurs sitting around dreaming up number sequences.
We don’t want to encourage too much of that, but you know, a small amount of dreaming is fine. There are some people who try to get as many sequences as they can into the OEIS; they submit far too much stuff of marginal value. Let’s take the prime numbers. You can ask: “What are all the prime numbers that begin with 7?” Okay, that’s a sequence in the database. But then you could say, “What about all the prime numbers that begin with 763?” That’s obviously too contrived. But if you say, “What about all the prime numbers that contain 666, the ‘number of the beast’?” That’s in the database; they’re called “beastly primes.” Then you recall how when everyone had a fax machine, the fax number was often the one following the phone number. So if my phone number was 555-4440, then my fax would be 555-4441. Well, there was a discussion about including prime numbers that contain 667, the “fax number of the beast.” This is an example of going too far.
So the fax numbers of the beast aren’t in?
I don’t think so. Let me look this up while we’re talking. I can check them by name. Actually, the fax numbers of the beast are in. I sent in the sequence myself.
Your standards have risen since then?
They go up and down. I get so many sequences. Until about 2009, I had to process everything myself. I processed the first 180,000 sequences. Since then, it’s been a wiki and the editors do most of the work. I get called in to resolve disputes and have the final say.
You now get about 20,000 new sequences submitted each year—that’s an extraordinary amount.
Yes. It would be nice if you could mention in your article that we are overwhelmed with submissions and could use more editors. Editors don’t get paid, but they get first crack at interesting sequences.
Is it the articulation of a problem that makes a sequence interesting?
It could be that the problem is interesting and the person who sends it in doesn’t realize quite how interesting it is. Or the proposer realizes it’s an interesting question but doesn’t have the mathematical skills to deal with it, in which case he or she will be grateful for help. That’s resulted in a lot of joint papers, when one of our editors has collaborated with some submitter to study a problem formally. This is one of the reasons for submitting a sequence: somebody may see it who might be able to help you work out the formula or algorithm for producing it.
OEIS reference number A131645
6661, 16661, 26669, 46663, 56663, 66601, 66617, 66629, 66643, 66653, …
The “beastly primes”—the sequence of prime numbers that contain the substring 666, “the number of the beast.”
OEIS reference number A138563
667, 1667, 2667, 3667, 4667, 5667, 6667, 6670, 6671, 6672, …
The sequence of prime numbers that contain the substring 667, “the fax number of the beast.”
OEIS reference number A245045
3, 11, 17, 43, 67, 113, 131, 193, 241, 353, …
This prime sequence by Chai Wah Wu consists of prime numbers n, such that for some integer k,
n =
Making k=1, 2, or 3 does not give a prime.
But when k=4, n=18/6=3, which is a prime.
Thus, 3 is the first term in the sequence. When k=8, n=66/6=11, so this is the second term,
and so on.
OEIS database reference number A254337
0, 1, 8, 6, 10, 14, 12, 4, 20, 16, …
This remarkable new sequence, submitted in February 2015 by Maximilian F. Hasler—a physicist and mathematician at the Université des Antilles et de la Guyane, Martinique—is one of Sloane’s all-time favorites. Here is its definition:
No term in the sequence is a prime.
No sum of 2 consecutive terms is a prime.
No sum of 3 consecutive terms is a prime.
No sum of 4 consecutive terms is a prime, and so on …
No term repeats any previous term.
For any term, always pick the nextsmallest number that fits the above rules.
Here is how we calculate the first few terms:
We start with 0, then 1, so the sequence begins 0, 1.
The next term cannot be 2 or 3 because they are prime.
It cannot be 4 either because 1+4=5 which is prime, and so it is not 5 either.
It cannot be 6 because 1+6=7, which is prime, and so it is not 7 either.
It can be 8. So it must be 8.
Thus the first three terms are: 0, 1, 8.
What is the fourth term? Given that we always have to choose the smallest number possible that has not been used before, we see that it cannot be 2, 3, or 5 (all prime), and it cannot be 4, because 1+8+4=13 which is prime. However, it can be 6, which is not prime, because 8+6=14 and 1+8+6 =15 (neither of which is prime).
Thus the sequence begins: 0, 1, 8, 6.
Mathematicians believe that in this sequence there are no odd numbers aside from 1, and that all even numbers greater than 2 appear. According to Sloane, “there is no proof yet for either of these conjectures and this may be a problem that’s too hard for twenty-first-century mathematics to handle.” Hasler’s sequence is like a new version of Fermat’s Last Theorem, something that is very simple to state but requires deep excursions into the foundations of mathematics to prove. Like Fermat’s theorem, this problem belongs to the domain of number theory, one of most difficult branches of mathematics. In an age when physicists have mapped the edges of the cosmos and created Higgs bosons, it is sobering to learn that mathematicians are still finding such richly confounding material in basic numerical games.


Let’s talk about a sequence recently submitted by Chai Wah Wu that is very enigmatic. It’s about prime numbers and it has a kind of elegance that made me think it might be one the great mathematician Leonard Euler would have come up with in the eighteenth century. Who is Chai Wah Wu?
He’s an engineer at IBM and a Fellow of the IEEE (Institute of Electrical and Electronics Engineers). He’s submitted, and edited, a lot of sequences, and he’s added programs for computing terms of many sequences, which is very useful. If I see a submission by him, I have a high degree of confidence it will be worthwhile.
His prime number sequence seems like something that should have been known to mathematicians before, but I suppose the OEIS is showing us that there are still many basic unsolved questions in mathematics.
Absolutely. Mathematics is always expanding. There are more powerful techniques, we look at more complicated problems, and this kind of question about sequences of primes with certain properties is of continuing interest. You are right, Euler would have been interested in this. Some of the most recent developments in mathematics have to do with sequences of prime numbers. It’s a very hot topic.
Can you give an example of a sequence that’s really odd or unusual?
Actually, I collect them. I keep notebooks where I jot them down and they now fill a bookcase. There’s one by Douglas Hofstadter, who wrote Gödel, Escher, Bach; he’s created quite a lot of interesting sequences. This one is called “Hofstadter’s Q Sequence.” It’s got a very simple rule. It’s a bit like the Fibonacci numbers, slightly different but similar in flavor. Someone has computed the first 1010 terms of this sequence, which is a lot! But there is no proof the sequence is infinite, so maybe at some point the computation ends and the sequence just stops. We don’t know. From a mathematical perspective, that’s remarkable.
Aside from being a lovely curiosity, is this likely to have any application in the world?
Oh, I shouldn’t think so.
Margaret Wertheim is the director of the Institute For Figuring, a Los Angeles nonprofit dedicated to the poetic and aesthetic dimensions of science and mathematics. Her latest book, co-authored with Christine Wertheim, is Crochet Coral Reef (Institute For Figuring, 2015); it documents the institute’s project in which thousands of women worldwide have joined in making a woolly archipelago of handicraft reefs as a collective artistic response to global warming.
Neil Sloane is a mathematician who worked for over forty years at AT&T. In 1964, he founded the Encyclopedia of Integer Sequences, which is now online and contains more than 260,000 sequences.
Spotted an error? Email us at corrections at cabinetmagazine dot org.
If you’ve enjoyed the free articles that we offer on our site, please consider subscribing to our nonprofit magazine. You get twelve online issues and unlimited access to all our archives.