Notes On Structure

­[T]hat music of the spheres which underlies each manmade system and every law of nature it is within our power to discern.
—Max Bill, The Mathematical Approach to Contemporary Art (1949)

Imagine yourself a fish at the center of a massive, seafaring school. You are driven by an instinctual urge to swim forward. Surrounded on all sides, you must at all times preserve a roughly sphere-shaped shell of open water around your body. This sphere is all that separates you from an avalanche of fish. It also comprises the outer limits of your perceptual field and, given that you are incapable of abstract thought, delineates the extent of your conscious being.

In “Fish Schools as Operational Structures,” noted ichthyologist Charles M. Breder, Jr. makes a confident assertion: “It is, of course, doubtful if creatures with well organized [sic] locomotor abilities and complex sensory systems are ever distributed in a fully random manner. The systems encountered in nature seem to be mostly those of ordered arrays variously distorted by processes of many kinds, sometimes obvious, but more often obscure or barely discernible.”^[1] On the strength of this assumption, Breder looks into the chaotic blur of the school and tries to see in it a latent structure. Bearing in mind those phenomenological fish spheres, he argues compellingly that schoolers arrange themselves not willy-nilly, but according to a specific geometric pattern.

At the outset, Breder employs the discipline of crystallography in his search for order, examining and quickly dismissing the face-centered cubic (FCC) lattice pattern. Arranged by this model, schools would display unnatural regimentation, like the files and ranks one sees upon passing an orchard, a marching band, or a Sol LeWitt sculpture. And yet, a close cousin of the FCC lattice provides a more accurate analog. Known as rhombic or hexagonal close-packing (HCP), this configuration can be envisioned, Breder notes, by “figuratively pushing the cubic lattice askew.” Place a fish sphere at each vertex of the lattice, taking care to point them all in the same direction, and we arrive at Breder’s theoretical school. Indeed, fish are often seen adopting something that looks like a crystalline structure, and suggestions of the rhombic lattice can be hard to miss.

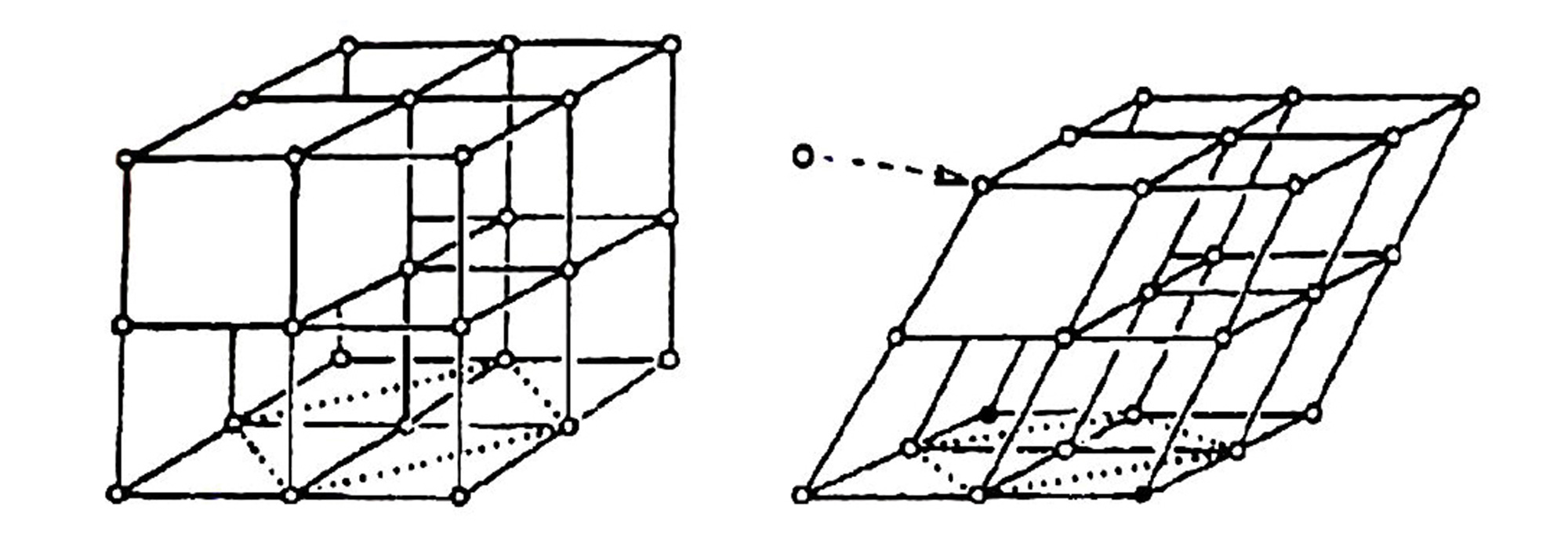
This hypothetical organization also happens to be that in which identical spherical objects can be made to pack together most densely within a given volume. For Breder, this naturally called to mind a line of mathematical inquiry known as “sphere-packing” or “the greengrocer’s problem.” Though ancient as the need to maximize the amount of grain stored in a single barrel, many of this field’s most fundamental questions were put to rest only with the advent of computers. The long-held intuition that spheres pack more closely in a rhombic lattice than when arranged helter-skelter has now been proven with near mathematical certainty.

Breder would surely have found recent work by a group of mathematicians led by Aleksandar Donev compelling. In “Improving the Density of Jammed Disordered Packings Using Ellipsoids,” the researchers demonstrate that the oblate spheroid—the shape of an M&M—attains a higher degree of packing density than the sphere.^[2] While fish bodies come in a great variety of shapes, fish that school often resemble sideways-flying versions of M&Ms, turned on their edges and variously elongated lengthwise. The researchers note in passing that unusually high densities are also obtained by the football-like prolate ellipsoid and the capsule-shaped spherocylinder, two other very fishy forms.

But why would fish want to spheroid-pack so closely as to approach Platonic mathematical ordering? Breder believes that the answer lies partly in schooling’s elusive hydrodynamic benefits: “The advantages of the regimented life in a school, as against the freedom of action common to the more or less solitary life, are evidently related to the effectiveness of the drag-reducing mucus in the vortices. The fishes with the least effective mucus appear to take advantage of the schooling life while those with the most effective mucus are more likely to be solitary.” In other words, the fluids released by each schooler’s body lubricate its fellows in water, reducing the ocean’s resistance to their inexorable onward push. Schooling fish close-pack, Breder argues, in order to immerse themselves in as much of their friends’ slime as possible.

Alas, due in part to the tedium of collecting sufficient quantities of fish snot for quantitative testing, “the mucus effect” remains largely unsubstantiated. More critically, recent research has shed doubt on Breder’s overall theory of “sphish-packing,” as computerized ocean-scanning technology has thus far failed to find definite lattice patterns in seafaring schools. With the verdict still out on rhombic pelagic packing, new approaches in evolutionary biology have of late prompted ichthyologists to focus less on the question of how fish school and more on why.^[3] Alongside better foraging potential, more accurate migratory route navigation, and ready availability of wanton sex partners, the benefits of schooling behavior include what is referred to in ichthyological parlance as a “repertoire of cooperative escape tactics.” Evincing fractal-like relationships between the individual spheroidal fish unit and the quasi-spherical form of the school as a whole, these maneuvers are often stunning to behold.

A predator approaches your school. First, the group nonchalantly allows him to penetrate. Once inside, he is literally stupefied by a blaze of bright, shiny objects. By the time he has recovered his overloaded senses, you have all slipped past him. But he persists, striking again, and suddenly your personal sphere buckles on one side. Like a startled driver on the interstate, you veer away from the impending collision, spilling into the spheres of your immediate neighbors. You are in the throes of the Trafalgar Effect, a wave of body-language cues that cascades outward from the predator’s location to the far edges of the school, alerting all to the presence of danger almost instantaneously.

Along with every last fish in the group, you now shift gears, making a desperate push toward the center to shield yourself with the bodies of your peers while they occupy the dangerous margins. Via this response, known as the “selfish herd mechanism,” the whole school collapses into a dense ball, and for a moment the predator is cowed by the sudden transformation of his bite-size snacks into what appears to be a monstrous, single fish. Should he strike again regardless, you have at your disposal the tactic of “flash expansion” (or the “burst effect”): With lightning speed and impeccable coordination, the school explodes into a million silver pieces, leaving the predator empty-mouthed and flabbergasted. You are safe now, but hardly have you had a chance to relish the victory when you realize that you are utterly alone. Obligate schoolers like yourself (a.k.a. “obligatorily gregarious” fish) tend to panic when separated from the collective. Hence after swimming a short distance, the school rushes to reassemble, recovering its order, though the relative positions of each fish are entirely reshuffled.

Not unlike fish overcome by existential dread at the prospect of facing the open ocean alone, humans, too, desperately crave the orderliness and predictability that schooling behavior represents. To quote ichthyologists Pierre Fréon and Ole Arve Misund, “the idea that schooling individuals pack in a certain complicated structure is appealing.”^[4] There is something intrinsically likable about the notion that the world is animated by secret, organizing forces. Indeed, we are neurobiologically equipped to perceive them. Take gestalt sensations, those cognitive operations by which the mind fills in missing information about the shape or organization of a given object or objects (say, a group of fish) so as to generate an impression of continuity or wholeness. As difficult as it is to describe this utterly pre-verbal phenomenon with words, it can be easily conveyed with the help of the classic diagrams of gestalt theory, such as the one in which we see not the reality of three Pacmen but a fictive triangle that partially obscures three fictive circles. A better representation of the way gestalt processes operate in the disorderly real world would be a frenzied school of Pacmen, somewhere within which lies a latent phantom triangle awaiting a spectator to perceive it into existence.

Around the time that Dr. Breder was trying to “see through the noise” of the fish school to its underlying slanted cubes, the art world was just getting over a serious cognitive hangover caused by more than a decade’s worth of viewing polyhedrons designed to elicit similar visualizations.^[5] Like Breder, many Minimalist artists spent much of the 1960s comparing objects (or groups of objects) situated out in the world against their gestalt understanding of geometric structure. An elucidating comparison can be drawn between “Fish Schools as Operational Structures” and Untitled (Mirrored Cubes), 1965, by Robert Morris. Whereas Breder begins with a natural setting and extrapolates from it a supposed latent geometry, Morris works in the reverse direction, starting with a set of geometric forms and half burying them in the world (not literally, of course, but vis-à-vis the spectator’s perceptual experience). In a typical gallery or museum, Mirrored Cubes argues with the floors and surrounding white walls, invoking institutional critique. In a grassy field, it pits the chaotic natural world against the orderliness of pure geometry. Outdoors, the cubes are unsettling not only because we are evolutionarily predisposed to feel a jolt of dissonance in the presence of unresolvable ambiguities between figure and ground (between Seen and Unseen, Known and Unknown), but also because, as Breder tells us, “ordered arrays” are rarely observed in nature; they are supposed to be “barely discernible.”

In his essay “Notes on Sculpture, Part 1,” Morris writes: “In the simpler regular polyhedrons, such as cubes and pyramids, one need not move around the object for the sense of the whole, the gestalt, to occur. One sees and immediately ‘believes’ that the pattern within one’s mind corresponds to the existential fact of the object. Belief in this sense is ... a kind of faith in spatial extension.” On a cue from phenomenologist philosopher Maurice Merleau-Ponty, Morris uses gestalt sensations to imply that our unconscious confidence in the know-ability, wholeness, and order of the world is unjustified, since it is premised to some extent on perceptual leaps of faith, and thus on leaps of logic. The ultimate aim is to instill in us, if only for an instant, the deepest possible kind of doubt: Should we really take for granted the truth of those views on the world that our brains glean from our retinas? With respect to the question of whether the universe comprises a celestial clockwork or just a heaping pile of chaos, Morris’s cynicism stands as a word of caution about the natural bias, the wishful thinking, that is secretly hardwired in our minds.

The universe would be truly depressing were it not for an occasional echo of the “music of the spheres,” and it’s no wonder that so many like Breder have attempted to discern it. A notable confrère is R. Buckminster Fuller, who shares with Breder not only nearly the same lifespan (Breder was born in 1897, just two years after Fuller; each died in 1983), but a fascination with sphere-packing and HCP lattices. While Breder applied his interest to fish schools, Fuller employed the phenomena to establish “Synergetics,” a baroque theory of the universal structures that ostensibly govern the cosmos.^[6] Fuller was of course the messiah of the sphere, which when close-packed provides the blueprint for his geodesic dome. Enervated by “geodesic tensegrity,” this structure is ultra-stable, purely as a function of its innately tense architectonics. Extremely large and sturdy domes can be built out of materials as light as paper tubes and Dacron thread and held together without knots, nails, bolts, or struts. The consummate humanitarian visionary, Fuller predicted that the principles underlying his geodesic constructions would save “Earthians” from inevitable extinction by environmental damage, overcrowding, and weapons of mass “killingry.”

Fuller’s grand schemes might seem a bit out there. But just two years after his death, an experiment carried out by a group of chemists seems to validate some of his weirdest theories.^[7] In the process of vaporizing graphite with lasers in an effort to replicate conditions inside red giant stars, Drs. Smalley, Curl, and Kroto accidentally produced copious amounts of a “remarkably stable cluster consisting of 60 carbon atoms.” Basing their analysis directly on Fuller’s ideas, they concluded that this species of carbon molecule could only have the form of a truncated icosahedron—Fuller’s geodesic sphere. The researchers dubbed the C60 structure “buckminsterfullerene” and in 1996 won the Nobel Prize in chemistry for its discovery.^[8]

So far, buckminsterfullerene has shown its greatest promise in breeding further esoteric physics research (probing the quantum-mechanical wave-particle duality of matter, for example). But many important utilitarian applications have been predicted for its future—from making vastly more powerful batteries to high-capacity spaceship fuel. At very low temperatures, it is a superconductor, conducting electricity with zero resistance. Buckminsterfullerene also has potential medicinal uses. Apparently, its distinctive soccer-ball form fits perfectly into the receptors of certain protease enzymes, blocking their activation sites, so C₆₀ can theoretically inhibit the production of the proteins the HIV virus needs to replicate itself.^[9] Thus a nanostructure that fits snugly in the human body was discovered in the attempt to imitate processes that occur in the bellies of red giant stars, at an enormous scale and mind-bogglingly far away—somewhere out there in the cosmos.

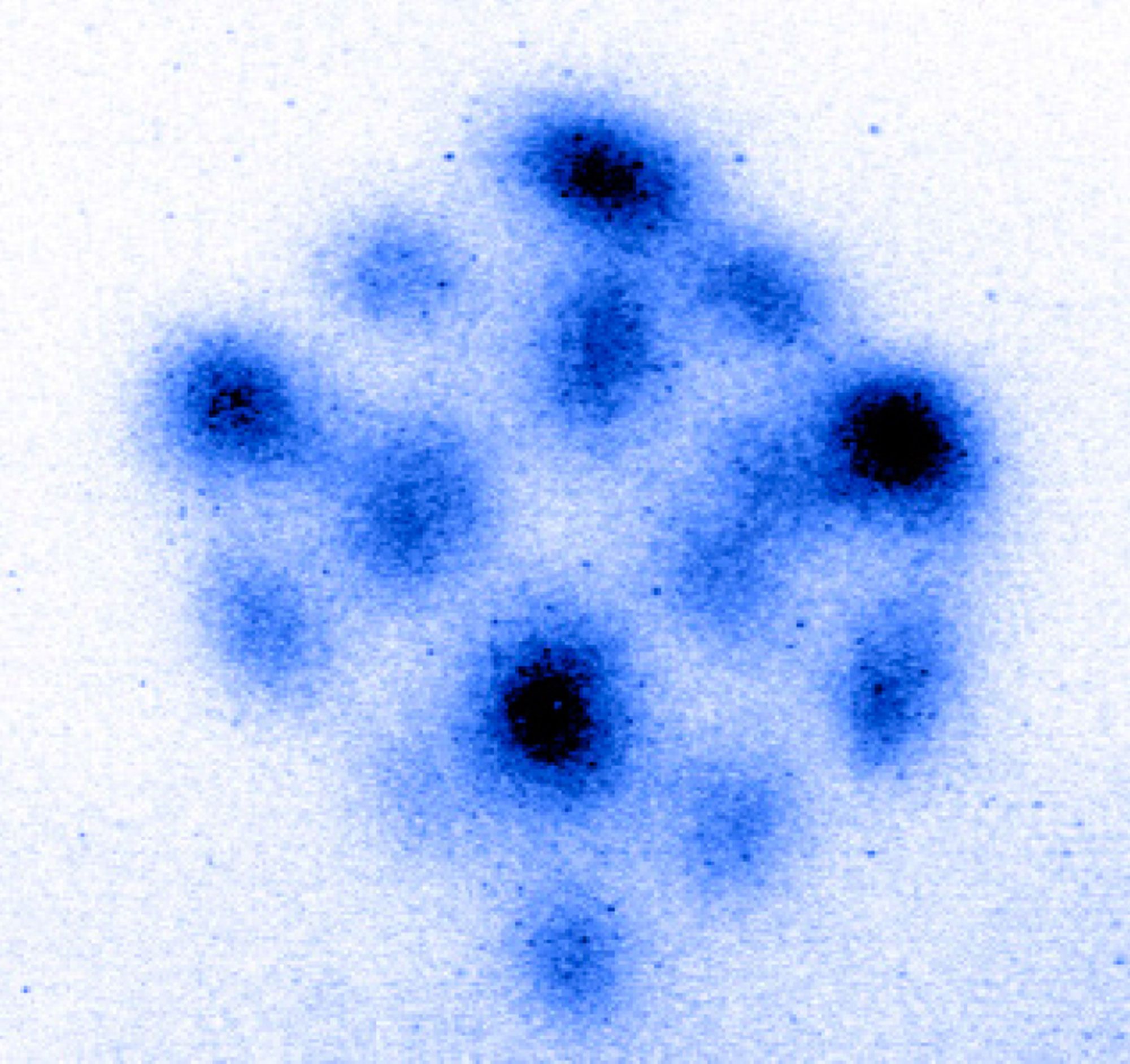
Without diminishing the considerable effort it took to stumble upon this connection, it was not anything Dr. Smalley and his colleagues could have predicted when they turned on their lasers. As is often the case with explorations at the atomic level, luck played a crucial role. Another serendipitous breakthrough along these lines brings us full circle, back to Breder’s lattice: Last year, a group of physicists supercooled a cloud of strontium atoms, subjecting them to unfathomably cold temperatures (roughly minus 450 degrees Fahrenheit, only millionths of a degree above absolute zero).^[10] They did so by irradiating the cloud with laser light, submerging the atoms in an “optical molasses” that greatly reduced their random kinetic energy. Utilizing three lasers focused on a single point, the researchers incidentally created an intersection of three planes. When the atoms aligned with the laser beams, like Breder’s phantom fish formation they unexpectedly took on the form of a cubic lattice. What better than this perfect, die-shaped accident—a supercool blend of latent cosmic forces, human intervention, and chance—to sum up the dream of an ordered universe?

At last, your school reaches deep water. You find yourself suspended amid a cold, black void, without reference to either surface or sea floor. Liberated from all contingency in the world, the school restores its primary shape, blossoming from amoeboid into discoid into spheroid into sphere.^[11] The area of open space around you expands, and you instinctually increase your speed. You are a unit in harmony with untold numbers of identical units, keyed into the ecstasy of synchronized flow. Now, once again, there is only the drive to swim onward.