Why Things Don’t Fall Down: An Interview with Robert Connelly
The forms and functions of tensegrity
Margaret Wertheim and Robert Connelly

In the autumn of 1948, while experimenting with ways to build flexible modular towers, a young artist named Kenneth Snelson constructed a sort of sculpture that had never been seen before. Ethereal in appearance and with no obvious weight-bearing elements, it nonetheless retained its shape and stability. The following summer, Snelson showed the form to his mentor, R. Buckminster Fuller, who had also been thinking about the possibilities of structures held together by tension. Fuller adopted Snelson’s invention as the centerpiece of his system of synergetics and, acknowledging its integrity under tension, gave it the name tensegrity. Tensegrities are manifest in such diverse structures as geodesic domes, cabled roofs, robotic arms, and spider webs, while analytical methods derived from understanding these forms are now shedding light on such scientific questions as how proteins fold and how glassy materials behave. In the 1970s, mathematicians began a systematic study of tensegrity structures, creating a theory with particular regard to their geometry. Robert Connelly, a mathematician at Cornell University and an expert on the mathematics of rigid and flexible frameworks, is a pioneer of this field. Using the mathematics of group theory, Connelly and his colleague Allen Back have compiled a catalogue of “super-stable symmetric tensegrities,” and in 1998 Connelly was part of the team that proved the famous “carpenter’s rule conjecture” using the idea of anti-tensegrity. In May 2005, he gave a talk at the Institute For Figuring in Los Angeles, in which audience members built and explored their own tensegrities. (A version of this talk will be delivered by Connelly on 20 November 2006 in New York at an event co-organized by Cabinet and the IFF and hosted by the Kitchen.) The interview below was conducted by IFF director Margaret Wertheim over the phone.
Cabinet: Can we start off with a little history? How did Snelson and Fuller come to the idea of tensegrities?
Robert Connelly: As I understand it, there was a workshop at Black Mountain College where Fuller was a teacher and Snelson was a student. At that time, Snelson discovered or created some structures he thought were interesting and showed them to Fuller. The first thing Snelson built was a kind of X shape, with wires around the outside; the X’s cross in the middle and you connect wires or strings or rubber bands around the outside. It’s a very simple structure but really quite intriguing. Over the years, he’s made a career out of building very large and complex tensegrities all over the world, including a sixty-foot-high structure at the Hirshhorn Museum. They’re wondrous things, made of thick aluminum tubes connected by high-gauge steel cable under an enormous tension. If you touch them, they kind of vibrate and you wonder how the thing can hold up. Fuller gave them a clever name, lectured about them, and thought about them as the basis for a lot of different structures and how they related to things in the world around us.


What does the term tensegrity mean?
One way of understanding tensegrity is that it’s a pattern that results when the pushes and pulls within a structure have a win-win relationship with each other. The pull is balanced by the push, producing integrity of tension and compression. Snelson’s idea was for a structure made of bars or struts suspended by cables—the cables are under tension and the struts are under compression. The tension in the system is the “tense” part, and the whole thing was stable—it didn’t fall down—so that’s the “integrity” part, hence the term tensional integrity.
How do mathematicians understand tensegrities?
It depends on the mathematician you ask. The way I think of it is quite simple: you have a bunch of points connected by lines, some of the points are allowed to get closer together but not further apart—these are what we call the “cables”—but other pairs of points are allowed to get further apart but not closer together—those are the “struts.” These rules put constraints on the system that determine what shape the structure can be overall. In the physical world, we don’t think of struts as things that are only allowed to get further apart; they’re objects that have fixed length. But for the mathematical study of tensegrities, you have one set of objects that can stretch (the struts) and another that can shrink (the cables)—the cables are under tension, and the struts are under compression.
What is specifically interesting for a mathematician about these structures?
They’re of interest to me because it’s a basic part of geometry. You have points floating around and you have distance constraints between the points, and the question is, “How do these constraints determine the configuration?” One example is a spider web. An interesting question is, “Why are spider webs rigid?” Are they rigid? Spider webs were the beginning point for me. It turns out that you can think of a spider web mathematically as a bunch of cables attached to some fixed points in space and the question is whether a particular configuration is going to flop around or is it going to hold its shape? It turns out that the secret is tension. If there’s tension everywhere in the web, it will hold its shape. That’s all you need. If there isn’t tension, it won’t. That’s a complete description of the tensegrity of a spider web.
There is a very nice theorem, that got me interested in this subject, known as the “rigidity conjecture,” which goes back at least to the Swiss mathematician Leonard Euler in the eighteenth century. The rigidity conjecture looks at closed surfaces, but not smooth continuous surfaces; rather, ones made up of triangular pieces joined at the edges— what we call triangulated surfaces. A complete geodesic sphere would be a closed triangulated surface. The conjecture was that if you have such a surface, it would be rigid; it could not wiggle about or change its shape at all. For over a century, mathematicians believed this was true for all cases, but in 1977 I actually found a counter-example. So that got me thinking about why anything keeps its shape and what are some general principles that you can use to show why things do or don’t keep their shape.
This is a critical subject for engineers; haven’t they been developing a formal study of how things keep their shape, and what conditions are necessary for that?
Of course engineers build buildings and spaceships and cars and boxes—billions of things. But when I started looking at what the principles were that they were using to show these things are rigid, frankly I was perplexed. Engineers seemed mostly concerned with giving examples, but, at first, didn’t seem to have a set of general principles. On looking into the matter more closely, I realized that an underlying principle in all structures was energy. Think of a spring: it takes energy to push it from its rest position. Many structures, including springs, tend to go into a configuration of minimal energy. A very basic principle that goes back to the great mathematicians Euler and Lagrange in the eighteenth century is that if a system, such as a set of springs, is in a state of minimal energy, it will be rigid. The first thing I did was to apply this principle to spider webs, and I found that it worked beautifully. The trouble was that the mathematics I used, which I thought was cool from the point of view of geometry, didn’t seem to make much sense from the point of view of real-world physics. So I went back and talked to the engineers because clearly the math worked, and it got answers.
What was so good about this mathematics you discovered?
Here’s a way to think of it. Imagine you have a tripod sitting on the ground with its three feet. It’s very stable—if you push, it pushes back and maintains its shape. The tensegrities Snelson built are more complex—if you push them they change their shape. Think of a clothesline strung between two buildings, a weightless clothesline. Now suppose you attach a shirt in the middle. The shirt pushes down, and the clothes-line will yield to that force and go down a bit until the forces restabilize. A tensegrity is more like a clothes-line than a tripod, and you have to consider non-linear factors. My mathematical energy function was good because it used very simple equations to describe this situation, equations that are not trivial, but simple.
How will this mathematical understanding of tensegrities help engineers?
Engineers often don’t feel comfortable building structures that look like Snelson’s tensegrities because they’re kind of wiggly; they can vibrate in funny ways. If one of the cables breaks or something gets struck, the whole structure can deform. But tensegrity is a useful idea for certain kinds of structures—roofs, for example, are often built on tensegrity principles. This mathematics would help engineers with structures that are Snelson-like, in the sense that they are under tension, like the clothesline or a spider web. It would help with the analysis because it’s a computational question where you can hopefully simplify the calculations so that it’s easier to tell whether the structure is stable or not.
Will the math you are developing help engineers build new kinds of structures?
Possibly. I have a catalogue of symmetric tensegrity structures, and I’ve arranged it so that with my analysis I can tell you that these things are nicely stable. That’s not always true with tensegrities. Sometimes you can make structures that look like they’re going to be okay, but then if you build them they get a little too wiggly. My analysis is slightly different from what most engineers are used to, which is why I’m writing a book with my colleague Simon Guest. We’re trying to bridge this divide between the mathematics and the engineering communities so that both groups can talk to one another.
Aside from designing buildings, are there applications of your work to other practical problems?
One possibility is protein folding. That’s a big subject a lot of people are working on right now. Mother Nature creates these long molecules, and somehow, as the molecule is being built, it wiggles its way out of the cell and forms a particular shape; that shape causes it to have some function, chemical or biological. In principle, the forces and energies are pretty well understood, but when people try to model proteins, it turns into a big mess. I think this is tailor-made for tensegrities, and the geometry and theory that go into them.
Another example is having better mathematical models for understanding how glassy substances behave. As materials, glasses are very random; the atoms or molecules get connected in a random way, so they are hard to model, unlike crystals where the arrangements are highly ordered. There are groups of chemists and physicists interested in trying to model glasses, and one thing they have done is to use a rigidity model. On a computer, you start with a network of points—think of a lattice made up of triangles stuck together. Now if you regard this lattice as made up of solid bars, it’s rigid. But what happens if you cut away some of those bars randomly? If you take away too many, the thing becomes floppy. The question is, “How many can you take away before it becomes floppy, and when does it change from being rigid to floppy?” Rigidity theory allows people to quickly compute whether a structure is rigid or not, and that has been very valuable. That work looked at two-dimensional lattices, and one interesting question is whether we can do a similar analysis with three-dimensional lattices, which is a much harder problem. The math I work on may help solve this question.
You were involved in solving the famous carpenter’s rule problem using ideas that came from the analysis of tensegrities. What is this problem?
You can think of it like protein folding in flatland. You have a chain of sticks strung together, just like a classic carpenter’s ruler. Now imagine you folded a really long carpenter’s ruler on a tabletop, in a very complicated pattern, but with no crossings. The question is, can it always be straightened out, or are there configurations where it gets locked up and can’t be unfolded? For a long time, people found all sorts of clever configurations that seemed to be locked. But it turned out some other guy would always come along and say, “Here, I can open it.” Günter Rote in Berlin, Erik Demaine, who’s now at MIT, and I worked on the problem and we proved that you could open up any configuration. Our theory involved a little-known result from the nineteenth-century physicist James Clerk Maxwell that was used by structural engineers to compute the forces in buildings. It showed that once you get started opening a folded ruler, there’s no stopping. One way of understanding this was that we were looking at the problem as if it were an anti-tensegrity, something that didn’t have a stable state.
Fuller had a conception that we’d all soon be living in tensegrity houses, particularly in geodesic domes, that we’d have whole cities sequestered in climate-controlled environments under enormous geodesic domes, and that we’d have space stations built inside giant tensegrity spheres. We don’t live in that world. Why haven’t tensegrity structures taken off in an everyday sense?
Basically, they have some serious practical drawbacks. When you build a big building, you start at the bottom and build your way to the top—you keep doing the same thing over and over. But if you build a dome, it can be tricky. The idea of having something that’s a kind of arch, where you have a true tensegrity in the sense of Snelson, where things are suspended—that’s awkward to build. On the other hand, there are buildings today built on the principle of having a shell on the outside and the shell provides the stability for the structure on the inside. That’s actually close to what the mathematician Cauchy did in 1813 that really pre-empted some of Fuller’s ideas. Personally, I think geodesic domes should be called Cauchy domes because he did the basic theory which showed why they hold up. Fuller’s domes are really just a specific instance of Cauchy’s basic principle. Another practical reason we don’t see more tensegrity-type buildings is that engineers, by necessity, are conservative. Just think if they said, “We’ll build a big building, it’s something nobody’s done before, but I’m pretty sure it’ll hold up. If it falls down, too bad.” That doesn’t really sell too well.
As someone who studies tensegrities formally, what do you think of Fuller’s visionary touting of these structures?
I think the reason for his popularity has a lot to do with his lack of concreteness or specificity. He’s been called a Yankee salesman, and it’s a bit like going to see fortunetellers. You think, “Wow, what they said was right on,” but mostly it’s because they said things in such a way that you can’t really say it was wrong. You just connect with what you think is relevant. I think Fuller was a master of that. He wasn’t really somebody like Newton or Maxwell who had a great new theory; he was somebody who said things that connected with people. As far as saying, “Well, I’m going to use his idea to build this building,” I don’t think you need that much of what he said. On the other hand, there are a lot of things he did build that were interesting, and in that respect, you can’t put him aside.
He’s having a renaissance at the moment in the art and architecture worlds. It’s interesting that the concept of tensegrity has an enormous resonance for so many people philosophically and aesthetically.
I agree and I think that’s not unreasonable. You can wax eloquent about the principles of tensegrities because they are the principles of structures, the principles underlying why things hold together.
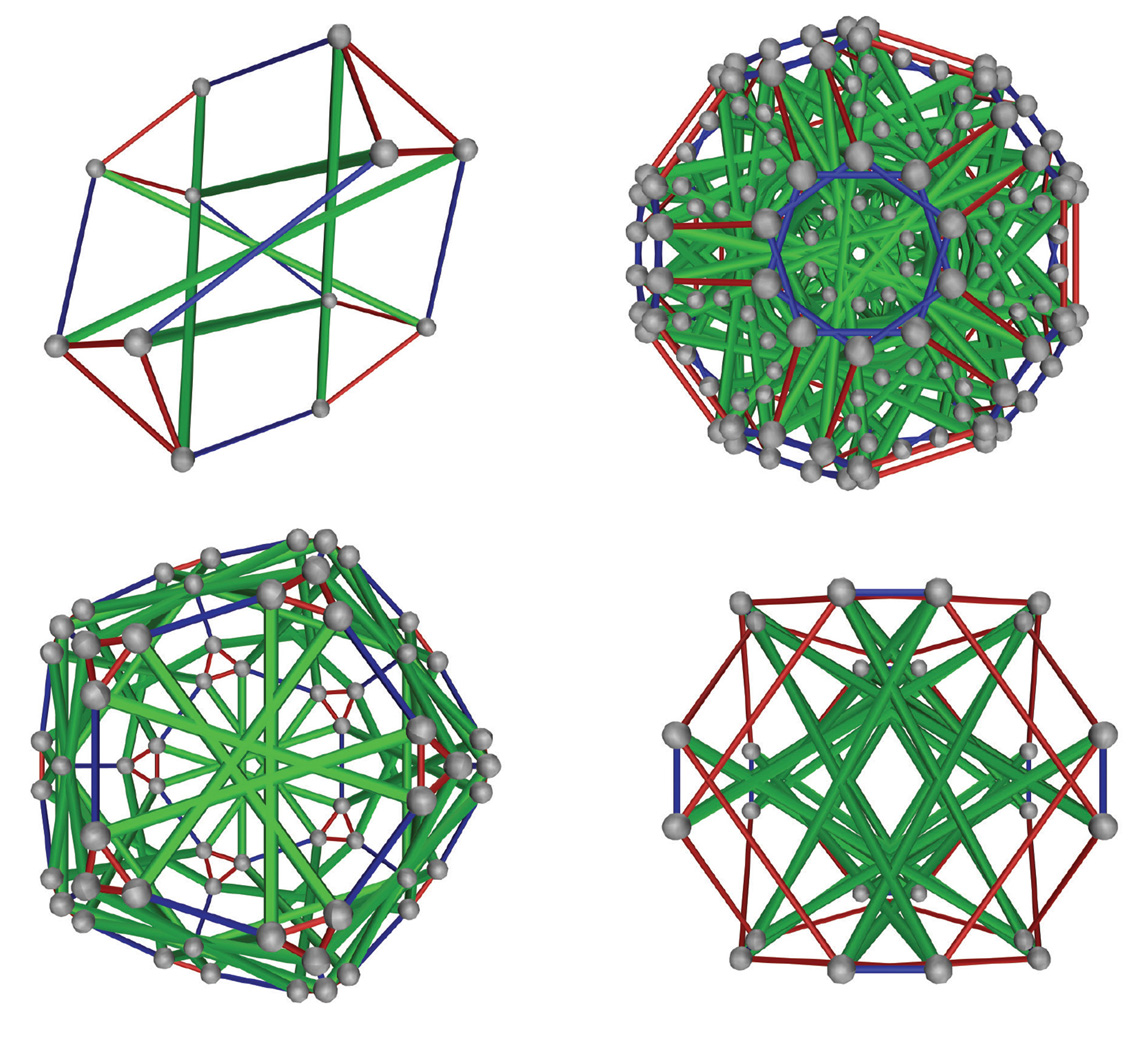
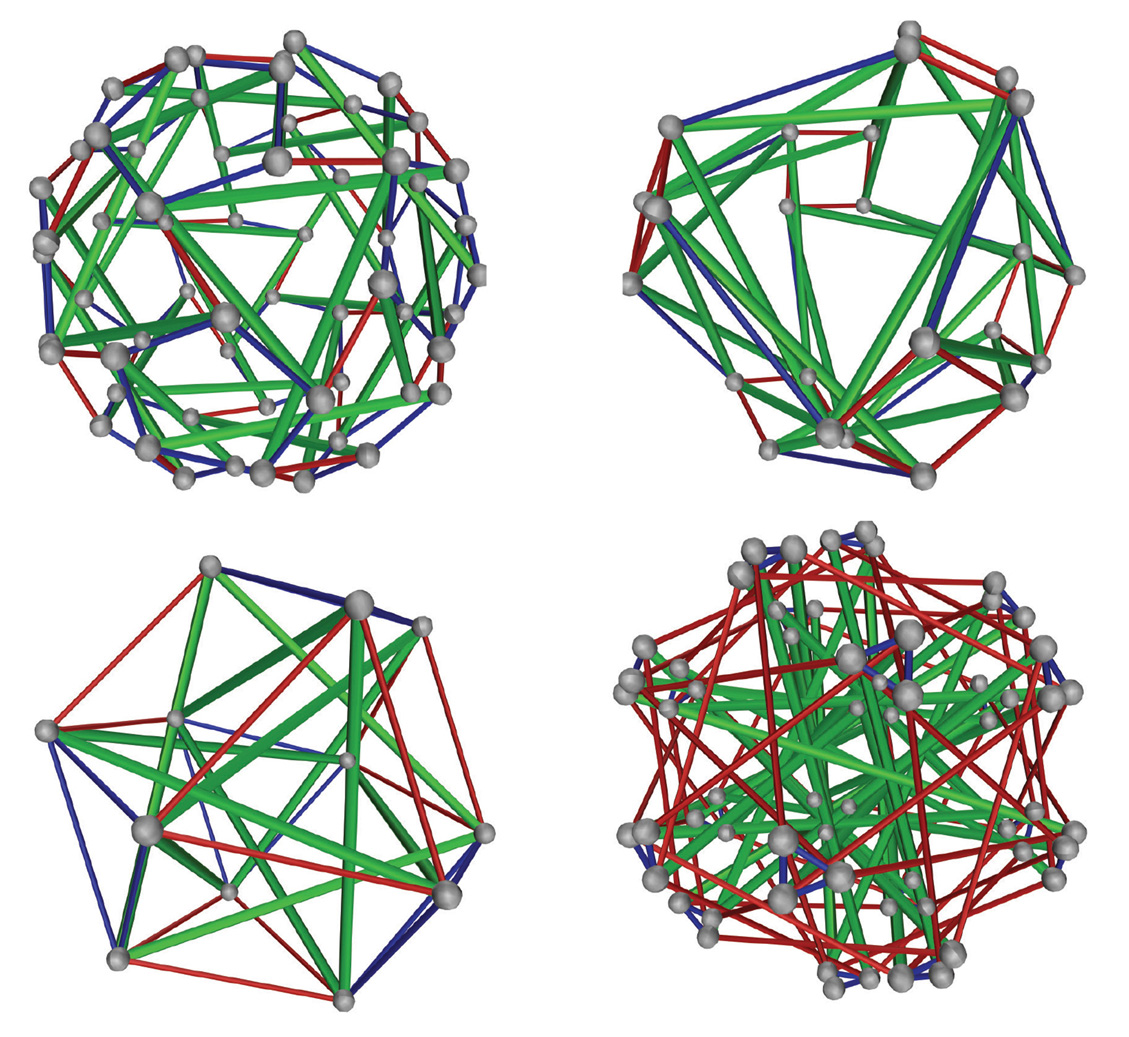
Robert Connelly, a professor of mathematics at Cornell University, received his Ph.D. from the University of Michigan in 1969 in geometric topology. Since then he has been interested in discrete geometry, especially the theory of rigid structures and its relations to other areas of geometry such as flexible surfaces, asteroid shapes, opening rulers, granular materials, and areas of unions of disks whose centers contract. He likes visual mathematics and the game of Go.
Margaret Wertheim is director of the Los Angeles–based Institute For Figuring, an organization devoted to enhancing the public understanding of figures and figuring techniques. Also a science writer, she pens the “Quark Soup” column for the LA Weekly, and is currently working on a book about the role of imagination in theoretical physics. See www.theiff.org.
Spotted an error? Email us at corrections at cabinetmagazine dot org.
If you’ve enjoyed the free articles that we offer on our site, please consider subscribing to our nonprofit magazine. You get twelve online issues and unlimited access to all our archives.